Язык R и высшая математика для студентов-политологов — опыт построения практико-ориентированного курса (Никита Шалаев, OSEDUCONF-2024) — различия между версиями

;{{SpeakerInfo}}: {{Speaker|Никита Шалаев}}
<blockquote>
Студенты-политологи (как и в целом студенты социальных наук) обычно относятся к 
изучению высшей математики как к не нужной трате времени, поскольку перспектив 
применения этих навыков они не видят, а преподавание строится вокруг 
классического подхода «с бумагой и карандашом». 

Этот доклад будет посвящён 
попытке изменить    ситуацию в более продуктивную сторону через совмещение 
преподавания математики и изучения языка R и среды разработки RStudio. 

В рамках доклада будет рассмотрен опыт организации курса высшей математики, 
построенного на базе свободного и бесплатного программного обеспечения и 
ориентированного на решение практических задач, и 
интеграции его в процесс обучения в целом.
</blockquote>

{{VideoSection}}
{{vimeoembed|989890147|800|450}}
{{youtubelink|}}

{{SlidesSection}}
[[File:Язык R и высшая математика для студентов-политологов — опыт построения практико-ориентированного курса (Никита Шалаев, OSEDUCONF-2024).pdf|left|page=-|300px]]

{{----}}

== Thesis ==
Следует отметить, что вопрос «особого» подхода к обучению математике студентов по 
специальностям, относящимся к социальным наукам, возник не сегодня. Идея о том, что 
в данном случае нужен некоторым образом адаптированный курс, была реализована, к примеру, 
в учебнике Акимова (МГИМО)<ref name="akimov"><i>Акимов&nbsp;В.&nbsp;П.</i> Математика для политологов. Учебное пособие. 2 изд. М.: МГИМО-Университет, 2011.</ref>, О'Брайена и Гарсии (Саутгемптонский университет)<ref name="obrien">
<i>O'Brien&nbsp;R.&nbsp;J., Garcia&nbsp;G.&nbsp;G.</i> Mathematics for Economicst and  Social Scientists. Palgrave Macmillan, 1971.</ref>, 
Гилла (Калифорнийский университет в Дейвисе)<ref name="gill"><i>Gill&nbsp;J.</i>  Essential Mathematics for Political and Social Research,  Cambridge University Press, 2006.</ref> и 
других. Однако обычно речь идёт об  отборе конкретных областей математики, с которыми 
в социальных науках шанс встретиться выше. В остальном же преподавание построено вокруг 
классической модели обучения математике самой по себе, хотя по возможности и с 
приведением релевантных примеров из социальных наук (в основном, правда, экономики).

В то же время идея необходимости математики в социальных науках не вызывает сомнения, 
как бы ни казалось студентам, что выбранные ими специальности представляют собой тихие 
гавани, убежища, свободные от формул и вычислений. Здесь можно опереться на авторитетное мнение 
политолога Рейна Таагеперы<ref name="taagepera"><i>Taagepera&nbsp;R.</i> Making Social Sciences More Scientific: The Need for Predictive Models. Oxford University Press, 2008.</ref>, с точки зрения которого математика должна быть 
поставлена во главу угла при проведении исследований, в то время как довольствоваться математикой, 
«законсервированной» внутри готовых статистических процедур разных 
прикладных программ, есть путь глубоко пагубный и скорее вредящий прогрессу в исследованиях, 
чем способствующий ему — и при этом совершенно типичный в наше время.

Существуют, однако, и попытки сделать математику ещё «ближе» для студентов. Здесь можно упомянуть 
учебник Ахтямова (БашГУ)<ref name="ahtyamov"><i>Ахтямов А. М.</i> Математика для социологов и экономистов. Учебное пособие. 2 изд. М.:Физматлит, 2008.</ref>, где параллельно с подачей «классического» материала 
рассматривалась работа и решение задач с системой компьютерной алгебры <tt>Maple</tt>. 
Этот подход можно покритиковать разве что за выбор проприетарного (и довольно дорогого) 
программного обеспечения для нужд образовательного процесса. Однако все вышеперечисленные идеи 
легли в основание курса, являющегося предметом доклада. С одной стороны, в рамках этого курса 
особое внимание было уделено областям математики, которые представляют наибольший практический 
интерес для политологов (например, теория множеств и булева алгебра, и, как следствие, качественный 
сравнительный анализ —  <tt>QCA</tt>; разностные уравнения; экстраполяция и интерполяция данных). 
С другой стороны, для решения математических проблем было привлечено программное обеспечение — 
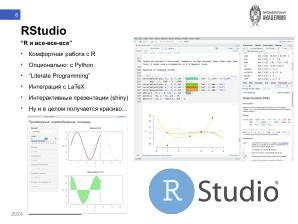
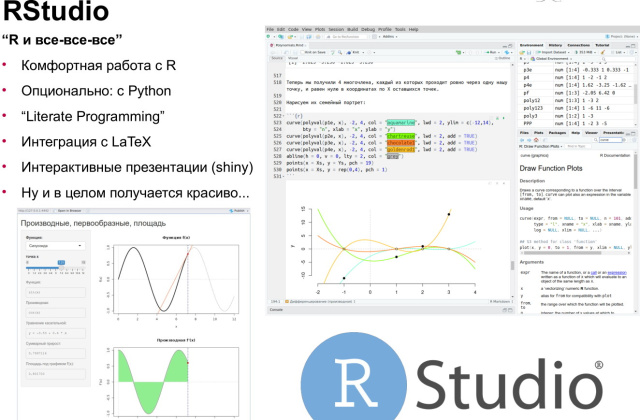
но уже свободное и бесплатное: язык  <tt>R</tt> и среда разработки  <tt>RStudiо</tt>, а также несколько 
«опорных» пакетов из арсенала  <tt>CRAN</tt> (прежде всего,  <tt>Ryacas</tt> и  <tt>pracma</tt>).

Выбор  <tt>R</tt> неслучаен. Во-первых, он широко используется в настоящих, полноценных исследованиях 
в социальных науках по своему прямому назначению — как язык статистического программирования. 
Поэтому изучая его, студенты изучают нечто, заведомо им полезное и в других областях профессиональной 
деятельности. Это выгодно отличает  <tt>R</tt> от 
более пригодных именно к математическим задачам систем компьютерной алгебры (например,  <tt>Maxima</tt>) 
или численного анализа (скажем,  <tt>GNU Octave</tt>). Кроме того, экосистема  <tt>R</tt> (прежде всего, 
репозиторий  <tt>CRAN</tt>) постоянно прирастают новыми пакетами, которые реализуют новейшие 
идеи и методы, позволяя пользователю оставаться на передовом крае науки. Во-вторых,  <tt>R</tt> и  
<tt>RStudio</tt> являются свободным и бесплатным программным обеспечением, что выгодно отличает их от 
проприетарных продуктов (<tt>Maple, Matlab, SPSS, STATA</tt> и&nbsp;т.&nbsp;д.), доступ к которым может оказаться 
потерян в любой момент по множеству причин, а в нормальных условиях потребует от студентов 
дополнительных трат после окончания обучения.  <tt>R</tt> же останется со студентами и после выпуска, 
безо всяких условий и ограничений, что в целом отвечает критерию 
фундаментальности и постоянства получаемых в стенах университета знаний. Наконец, в-третьих,  
<tt>R</tt> и  <tt>RStudio</tt> позволяют реализовывать концепции «грамотного программирования» и 
воспроизводимых исследований, в том числе в коллективе.

Конечно, в рамках курса пришлось пойти и на некоторые компромиссы. Так, например, был сделан выбор 
в пользу системы компьютерной алгебры <tt>yacas</tt>, так как она легко доступна в виде одного пакета 
(<tt>Ryacas</tt>), в то время как гораздо более мощная <tt>Maxima</tt> требует отдельной установки. 
Также большое внимание уделяется не только «первосортным» аналитическим методам и компьютерной 
алгебре, но и численным методам решения задач, для которых <tt>R</tt> приспособлен много лучше<ref name="howard"><i>Howard James P.</i> Computational Methods for Numerical Analysis with R. CRC Press (Taylor \& Francis group), 2017.</ref>.

С другой стороны, выявились и неожиданные преимущества от реализуемой схемы. Например, списывание 
оказалось легко выявляемым как при копировании кода между студентами, так и при выдаче им за свой 
труд кода, написанного кем-то ещё (возможно, как раз знакомым студентом какого-то технического 
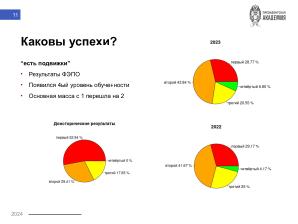
направления). И в целом по результатам тестирования ФЭПО отмечается последовательное улучшение 
результатов. Наконец, благодаря широким возможностям  <tt>R</tt>, эту же 
программную основу получилось повторно использовать и в других курсах: от теории игр до анализа 
государственной политики.


{{----}}
[[File:{{#setmainimage:Язык R и высшая математика для студентов-политологов — опыт построения практико-ориентированного курса (Никита Шалаев, OSEDUCONF-2024)!.jpg}}|center|640px]]
{{LinksSection}}
<!-- <blockquote>[©]</blockquote> -->

<references/>

[[Категория:OSEDUCONF-2024]]
[[Категория:Draft]]
[[Категория:СПО в образовании]]