Интерактивный конвертер Chipollino для наглядного изучения теории автоматов (Александр Дельман, OSEDUCONF-2023) — различия между версиями
Материал из 0x1.tv
StasFomin (обсуждение | вклад) (Новая страница: «;{{SpeakerInfo}}: {{Speaker|Александр Дельман}} <blockquote> </blockquote> {{VideoSection}} {{vimeoembed||800|450}} {{youtubelink|}} {{SlidesSe…») |
StasFomin (обсуждение | вклад) |
||
;{{SpeakerInfo}}: {{Speaker|Александр Дельман}}
<blockquote>
В теории формальных языков существует множество различных способов представить регулярные языки, начиная от классических конечных автоматов и кончая полугруппами преобразований. Знакомство с этим разнообразием представлений не только расширяет кругозор, но и формирует связь между различными областями теоретической информатики. Однако в рамках учебного курса на теорию автоматов отводится крайне мало времени, и попытка вместить в эти часы хотя бы базовые понятия о каждом из представлений приводит к тому, что они выглядят как мало связанные между собой разрозненные факты. При этом, если студент пропустил общеизвестную тему (например, по минимизации ДКА), его можно отправить «смотреть индусов», но некоторые из тем представлены в основном в специальной литературе, и если студент не успел понять такую тему на лекции, то он вынужден разбираться в ней по единственному примеру из слайдов или по статьям. Несложную и красивую теорию оказывается трудно оставить на самостоятельный разбор из-за недостатка наглядных материалов.
Изначально проект возник из намерения перенести некоторое количество теории в лабораторные работы, в связи с чем наряду с индивидуальными вариантами лабораторных появилась возможность взять групповую задачу. Наглядное представление было лишь одной из подзадач и в основном требовалось для отладки алгоритмов преобразования различных представлений друг в друга (тем более что студенты уже владели базовыми навыками использования <tt>Graphviz</tt> и зачастую сами добавляли вывод диаграмм в свои лабораторные работы). Чуть позже стало ясно, что если эту сторону проекта лучше развить, то им могут воспользоваться не только его непосредственные разработчики, но для этого недостаточно строить <tt>dot</tt>-представление автоматов, а также нужно демонстрировать промежуточные выкладки в форме таблиц, списков и пошагового описания преобразований. Эти представления удобно записывать в <tt>LaTeX</tt>. Окончательная конвертация диаграмм [https://github.com/kjellmf/dot2tex dot2tex] тоже осуществляется в <tt>LaTeX</tt>, с помощью библиотеки <tt>Tikz</tt>. Дополнительно к конвертеру, в частности, для упрощения тестирования, добавлен модуль порождения случайных регулярных выражений и задач.
* https://github.com/StarikTenger/Chipollino
</blockquote>
{{VideoSection}}
{{vimeoembed||800|450}}
{{youtubelink|}}
{{SlidesSection}}
[[File:Интерактивный конвертер Chipollino для наглядного изучения теории автоматов (Александр Дельман, OSEDUCONF-2023).pdf|left|page=-|300px]]
{{----}}
== Thesis ==
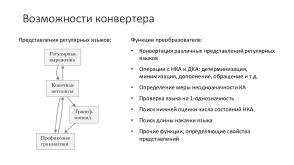
В настоящий момент конвертер охватывает следующие представления регулярных языков:
* регулярные выражения;
* недетерминированные и детерминированные автоматы;
* трансформационные моноиды;
* префиксные грамматики.
На вход конвертеру подаётся текстовый файл с последовательностью инструкций, преобразования по которым будут залогированы. Пример файла с инструкцией представлен ниже. Восклицательные знаки указывают, что преобразование логируется.
<pre>
R = {(aa*)*(a*)*a*b}
A = MergeBisim.Antimirov R !!
</pre>
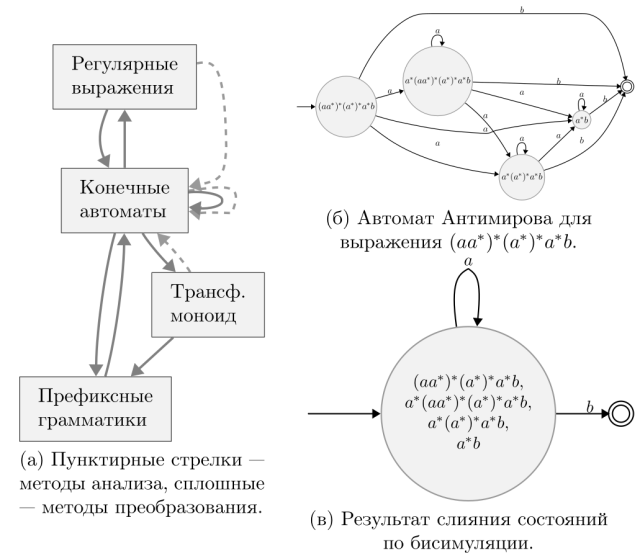
Результат преобразования регулярного выражения \verb|R| в автомат Антимирова посредством построения частичных производных и слияния по бисимуляции состояний в автомате представлен на рис. «Логика конвертера <tt>Chipollino</tt> и пример преобразований»:
[[File:Интерактивный_конвертер_Chipollino_для_наглядного_изучения_теории_автоматов_(OSEDUCONF-2023)-pic001.png|640px|center]]
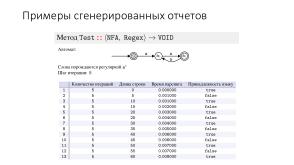
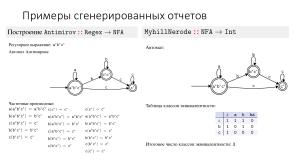
Большое количество различных представлений и возможность автоматически проанализировать лично построенный пример регулярного выражения позволяет на практике разобраться со свойствами преобразований, рассматриваемых в курсе<ref>Неисчерпаемое число взаимосвязей между различными преобразованиями в теории автоматов и вдохновило на идею проекта--конвертера.</ref>. Например, убедиться, что алгоритм минимизации Брзозовски (посредством цепочки обращений и детерминизаций) эквивалентен классическому алгоритму минимизации <ref><i>B. W. Watson</i> A Taxonomy of Finite Automata Minimization Algorithms // Computing science notes, Vol.9344, Technische Universiteit Eindhoven, 1993.</ref>, и сравнить их скорость для случайно порождённых автоматов; или что автомат Глушкова получается из автомата Томпсона после удаления пустых переходов<ref><i>C. Allauzen, M. Mohri</i> A Unified Construction of the Glushkov, Follow, and Antimirov Automata // TR2006-880, Courant Institute of Mathematical Sciences, 2006.</ref>. Ещё один интересный опыт был связан с поиском нижней оценки числа минимальных состояний в недетерминированном конечном автомате: эксперименты показали, что наиболее известная оценка из работы <ref><i>I. Glaister, J. Shallit</i> Lower Bound Technique for the Size of Nondeterministic Finite Automata // Information Processing Letters, 59, 75—77, 1996.</ref> может быть легко улучшена (и, оказывается, улучшение уже существовало <ref><i>J.-C. Birget</i> Intersection and Union of Regular Languages and State Complexity // Information Processing Letters 43, 185—190, 1992.</ref>, причём опубликованное в том же журнале, но из-за использования различной терминологии сходство было замечено не сразу).
Определённые сложности проекта связаны с тем, что изначально он задумывался как лабораторная работа, от которой не требуется таких качеств, как масштабируемость и удобный пользовательский интерфейс. Также из-за большого охвата теоретических конструкций не все из них пока что охвачены подробными логами — эта задача остаётся на будущее.
{{----}}
[[File:{{#setmainimage:Интерактивный конвертер Chipollino для наглядного изучения теории автоматов (Александр Дельман, OSEDUCONF-2023)!.jpg}}|center|640px]]
{{LinksSection}}
<!-- <blockquote>[©]</blockquote> -->
<references/>
[[Категория:OSEDUCONF-2023]]
[[Категория:Draft]]
[[Категория:СПО в образовании]] | |||
Версия 03:56, 18 января 2024
- Докладчик
- Александр Дельман
В теории формальных языков существует множество различных способов представить регулярные языки, начиная от классических конечных автоматов и кончая полугруппами преобразований. Знакомство с этим разнообразием представлений не только расширяет кругозор, но и формирует связь между различными областями теоретической информатики. Однако в рамках учебного курса на теорию автоматов отводится крайне мало времени, и попытка вместить в эти часы хотя бы базовые понятия о каждом из представлений приводит к тому, что они выглядят как мало связанные между собой разрозненные факты. При этом, если студент пропустил общеизвестную тему (например, по минимизации ДКА), его можно отправить «смотреть индусов», но некоторые из тем представлены в основном в специальной литературе, и если студент не успел понять такую тему на лекции, то он вынужден разбираться в ней по единственному примеру из слайдов или по статьям. Несложную и красивую теорию оказывается трудно оставить на самостоятельный разбор из-за недостатка наглядных материалов.
Изначально проект возник из намерения перенести некоторое количество теории в лабораторные работы, в связи с чем наряду с индивидуальными вариантами лабораторных появилась возможность взять групповую задачу. Наглядное представление было лишь одной из подзадач и в основном требовалось для отладки алгоритмов преобразования различных представлений друг в друга (тем более что студенты уже владели базовыми навыками использования Graphviz и зачастую сами добавляли вывод диаграмм в свои лабораторные работы). Чуть позже стало ясно, что если эту сторону проекта лучше развить, то им могут воспользоваться не только его непосредственные разработчики, но для этого недостаточно строить dot-представление автоматов, а также нужно демонстрировать промежуточные выкладки в форме таблиц, списков и пошагового описания преобразований. Эти представления удобно записывать в LaTeX. Окончательная конвертация диаграмм dot2tex тоже осуществляется в LaTeX, с помощью библиотеки Tikz. Дополнительно к конвертеру, в частности, для упрощения тестирования, добавлен модуль порождения случайных регулярных выражений и задач.
Содержание
Видео
Презентация
Thesis
В настоящий момент конвертер охватывает следующие представления регулярных языков:
- регулярные выражения;
- недетерминированные и детерминированные автоматы;
- трансформационные моноиды;
- префиксные грамматики.
На вход конвертеру подаётся текстовый файл с последовательностью инструкций, преобразования по которым будут залогированы. Пример файла с инструкцией представлен ниже. Восклицательные знаки указывают, что преобразование логируется.
R = {(aa*)*(a*)*a*b}
A = MergeBisim.Antimirov R !!
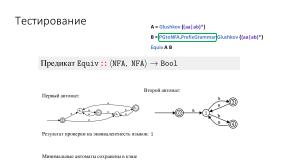
Результат преобразования регулярного выражения \verb|R| в автомат Антимирова посредством построения частичных производных и слияния по бисимуляции состояний в автомате представлен на рис. «Логика конвертера Chipollino и пример преобразований»:
Большое количество различных представлений и возможность автоматически проанализировать лично построенный пример регулярного выражения позволяет на практике разобраться со свойствами преобразований, рассматриваемых в курсе[1]. Например, убедиться, что алгоритм минимизации Брзозовски (посредством цепочки обращений и детерминизаций) эквивалентен классическому алгоритму минимизации [2], и сравнить их скорость для случайно порождённых автоматов; или что автомат Глушкова получается из автомата Томпсона после удаления пустых переходов[3]. Ещё один интересный опыт был связан с поиском нижней оценки числа минимальных состояний в недетерминированном конечном автомате: эксперименты показали, что наиболее известная оценка из работы [4] может быть легко улучшена (и, оказывается, улучшение уже существовало [5], причём опубликованное в том же журнале, но из-за использования различной терминологии сходство было замечено не сразу).
Определённые сложности проекта связаны с тем, что изначально он задумывался как лабораторная работа, от которой не требуется таких качеств, как масштабируемость и удобный пользовательский интерфейс. Также из-за большого охвата теоретических конструкций не все из них пока что охвачены подробными логами — эта задача остаётся на будущее.
Примечания и ссылки
- ↑ Неисчерпаемое число взаимосвязей между различными преобразованиями в теории автоматов и вдохновило на идею проекта--конвертера.
- ↑ B. W. Watson A Taxonomy of Finite Automata Minimization Algorithms // Computing science notes, Vol.9344, Technische Universiteit Eindhoven, 1993.
- ↑ C. Allauzen, M. Mohri A Unified Construction of the Glushkov, Follow, and Antimirov Automata // TR2006-880, Courant Institute of Mathematical Sciences, 2006.
- ↑ I. Glaister, J. Shallit Lower Bound Technique for the Size of Nondeterministic Finite Automata // Information Processing Letters, 59, 75—77, 1996.
- ↑ J.-C. Birget Intersection and Union of Regular Languages and State Complexity // Information Processing Letters 43, 185—190, 1992.