Chipollino — как лабораторная работа превратилась в инструмент для исследований (Александр Дельман, OSEDUCONF-2024) — различия между версиями
Материал из 0x1.tv
StasFomin (обсуждение | вклад) |
StasFomin (обсуждение | вклад) (→Thesis) |
||
== Thesis ==
* https://github.com/OnionGrief/Chipollino
Современная теория формальных языков — фундамент для освоения теории компиляторов, теории типов, алгоритмов
преобразования и анализа программ. Однако в части наглядных средств её освоения есть некоторые затруднения.
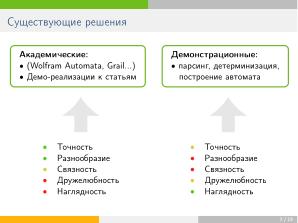
Актуальные теоретические работы зачастую лишены программных реализаций, или эти реализации удобны в применении только для разработчика
(теоретика, написавшего статью). Классическая теория автоматов на уровне элементарного курса представлена в
форме открытых программ достаточно широко, но реализации с удобным графическим интерфейсом иногда плохо
протестированы и имеют небольшой функционал. Поэтому возникла идея собрать воедино множество методов теории
автоматов так, чтобы удовлетворить потребность в наглядности, не теряя в широте охвата преобразований и их
корректности.
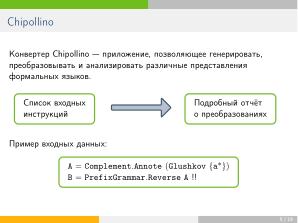
Изначально конвертер, включающий эти методы, представлял собой групповую лабораторную работу;
в дальнейшем в проект добавились результаты также нескольких курсовых работ.
Основные требования, предъявляемые к разработке:
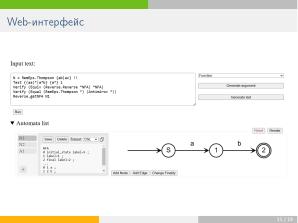
;наглядность: — результаты преобразований должны быть представлены в понятной пользователю форме.
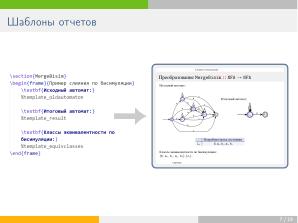
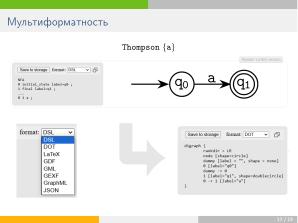
Для решения этой задачи в качестве базового представления сущностей был выбран язык <tt>LaTeX</tt> и библиотека \textsc{Tikz} для отрисовки автоматов. Эти средства наиболее выразительны, и из \LaTeX-формата нетрудно извлечь более простые посредством упрощающих гомоморфизмов.
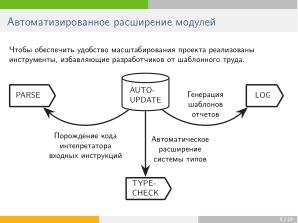
;расширяемость: — интерфейс должен быть достаточно удобен для пополнения новыми функциями и типами автоматов или других представлений формальных языков. Для решения этой задачи конвертер был спроектирован таким образом, чтобы модули синтаксического разбора, проверки типов и логирования допускали обновления посредством автоматического порождения необходимого кода (исключая «рабский труд» по написанию шаблонного кода).
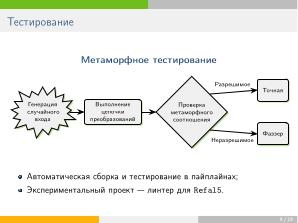
;связность: — должна быть возможность демонстрации соотношений между преобразованиями, а также их композициями. Для решения этой задачи было введено понятие цепочки преобразований, а также введены метод <tt>Verify</tt> (в пользовательском интерфейсе) и метаморфное тестирование<ref name="MetaTest"><i>T. Y. Chen, S. C. Cheung, S. M. Yiu</i>: Metamorphic testing: A new approach for generating next test cases // TR HKUST-CS98-01, Department of Computer Science, The Hong Kong University of Science and Technology, Hong Kong, 1998.</ref> (для разработчиков).
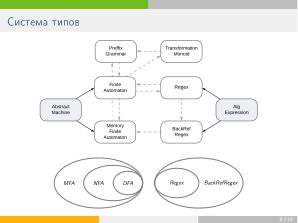
=== Экосистема проекта ===
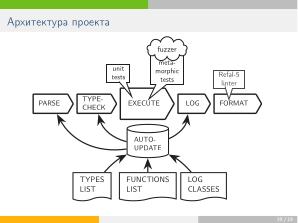
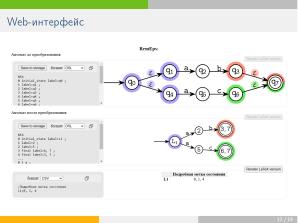
В связи с тем, что проект пополнялся не только методами, но и новыми классами автоматов (в частности, «PDA» — стековые автоматы; «MFA» — автоматы с памятью), было решено расширить его экосистему средствами автоматического обновления, позволяющими быстро добавлять в интерфейс новый функционал. В модуль автотестирования помимо юнит-тестов были добавлены метаморфные тесты, проверяющие инвариантность свойств объектов относительно цепочек преобразований. В силу того, что некоторые классы автоматов (в частности, «MFA») имеют неразрешимое отношение эквивалентности, был разработан также фазз-модуль, осуществляющий приблизительную проверку равенства языков соответствующих распознавателей.
Сам конвертер написан на языках <tt>C++</tt>} (большая часть фронтенда и весь бэкенд) и <tt>Refal-5</tt> (форматирующие скрипты для порождения \LaTeX-исходников). В связи с этим, отдельно стоит упомянуть экспериментальный проект Линтера для <tt>Refal-5</tt>,
который служит цели улучшить дисциплину кода, ранее не контролировавшуюся никем, кроме самого разработчика, делающего коммиты,
и находится на стадии встраивания в «CI» проекта.
=== Применение в исследованиях ===
Хотя изначально конвертер разрабатывался как чисто учебный проект, оказалось, что этот инструмент удобен и
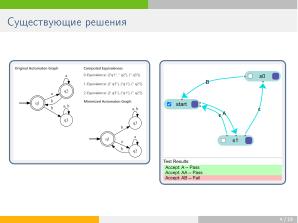
для теоретических исследований. В частности, посредством метода <tt>Verify</tt> удобно перепроверять
утверждения на предмет неявных допущений, что показал анализ статьи <ref name="Mohri"><i>C. Allauzen, M. Mohri</i>: A Unified Construction of the Glushkov, Follow,
and Antimirov Automata // TR2006-880, Courant Institute of Mathematical Sciences, 2006.</ref>, выявивший несколько неточностей
в приведённых формулировках. Кроме того, методы анализа полугрупповых структур показали хорошую скорость и
точность при выявлений «REDoS»-ситуаций в академических регулярных выражениях с перекрытиями в
подвыражениях<ref name="SYRCoSE23"><i>A. N. Nepeivoda, Yu. A. Belikova, K. K. Shevchenko, M. R. Teriukha, D. P. Knyazihin, A. D. Delman, A. S. Terentyeva</i> REDoS detection in ``Domino'' regular expressions by Ambiguity Analysis // Труды ИСП РАН 35(3), 109—124, 2023.</ref>, для которых методы анализа, использующие самопересечения автоматов <ref name="RSA"><i>N. Weideman, B. van der Merwe, M. Berglund, B. W. Watson</i>:{Analyzing Matching Time Behavior of Backtracking Regular Expression Matchers by Using Ambiguity of {NFA}} //Proc. of Implementation and Application of Automata - 21st International Conference, {Lecture Notes in Computer Science}, 9705, p.322—334, 2016.</ref>,
работают слишком медленно, а фаззеры<ref name="ReScue"><i>Y. Shen, Y. Jiang, C. Xu, P. Yu, X. Ma, J. Lu</i>: {Re{S}cue: Crafting Regular Expression DoS Attacks} // Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, 225—235, 2018.</ref>,<ref name="Revealer"><i>Y. Liu, M. Zhang, W. Meng</i>: {Revealer: Detecting and Exploiting Regular Expression Denial-of-Service Vulnerabilities} // Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), 1468—1484, 2021.</ref> — ненадёжно. Последним применением конвертера
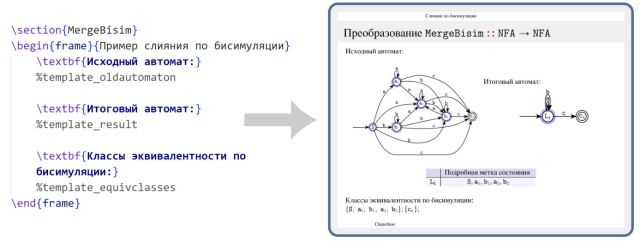
на данный момент стало исследование бисимуляций в конечных автоматах с памятью посредством аппроксимаций
классическими конечными автоматами<ref name="SYRCoSE24"><i>A. N. Nepeivoda, A. D. Delman, A. S. Terentyeva</i> Bisimulations in Memory Finite Automata // SYRCoSE 2024 Proceedings, 2024.</ref>. Поставленная цель — сделать осязаемыми абстрактные концепции, используемые в современной теории формальных языков, — оказалась полезна не только для сдачи
зачётов, но и для испытания новых гипотез.
{{----}}
[[File:{{#setmainimage:Chipollino — как лабораторная работа превратилась в инструмент для исследований (Александр Дельман, OSEDUCONF-2024)!.jpg}}|center|640px]]
{{LinksSection}}
<!-- <blockquote>[©]</blockquote> -->
<references/>
[[Категория:OSEDUCONF-2024]]
[[Категория:Draft]]
[[Категория:СПО в образовании]] | |||
Версия 20:00, 29 июля 2024
- Докладчик
- Александр Дельман
Современная теория формальных языков — фундамент для освоения теории компиляторов, теории типов, алгоритмов преобразования и анализа программ. Однако в части наглядных средств её освоения есть некоторые затруднения.
Актуальные теоретические работы зачастую лишены программных реализаций, или эти реализации удобны в применении только для разработчика (теоретика, написавшего статью). Классическая теория автоматов на уровне элементарного курса представлена в форме открытых программ достаточно широко, но реализации с удобным графическим интерфейсом иногда плохо протестированы и имеют небольшой функционал. Поэтому возникла идея собрать воедино множество методов теории автоматов так, чтобы удовлетворить потребность в наглядности, не теряя в широте охвата преобразований и их корректности.
Изначально конвертер, включающий эти методы, представлял собой групповую лабораторную работу; в дальнейшем в проект добавились результаты также нескольких курсовых работ.
Содержание
Видео
Презентация
Thesis
Современная теория формальных языков — фундамент для освоения теории компиляторов, теории типов, алгоритмов преобразования и анализа программ. Однако в части наглядных средств её освоения есть некоторые затруднения.
Актуальные теоретические работы зачастую лишены программных реализаций, или эти реализации удобны в применении только для разработчика (теоретика, написавшего статью). Классическая теория автоматов на уровне элементарного курса представлена в форме открытых программ достаточно широко, но реализации с удобным графическим интерфейсом иногда плохо протестированы и имеют небольшой функционал. Поэтому возникла идея собрать воедино множество методов теории автоматов так, чтобы удовлетворить потребность в наглядности, не теряя в широте охвата преобразований и их корректности.
Изначально конвертер, включающий эти методы, представлял собой групповую лабораторную работу; в дальнейшем в проект добавились результаты также нескольких курсовых работ.
Основные требования, предъявляемые к разработке:
- наглядность
- — результаты преобразований должны быть представлены в понятной пользователю форме.
Для решения этой задачи в качестве базового представления сущностей был выбран язык LaTeX и библиотека \textsc{Tikz} для отрисовки автоматов. Эти средства наиболее выразительны, и из \LaTeX-формата нетрудно извлечь более простые посредством упрощающих гомоморфизмов.
- расширяемость
- — интерфейс должен быть достаточно удобен для пополнения новыми функциями и типами автоматов или других представлений формальных языков. Для решения этой задачи конвертер был спроектирован таким образом, чтобы модули синтаксического разбора, проверки типов и логирования допускали обновления посредством автоматического порождения необходимого кода (исключая «рабский труд» по написанию шаблонного кода).
- связность
- — должна быть возможность демонстрации соотношений между преобразованиями, а также их композициями. Для решения этой задачи было введено понятие цепочки преобразований, а также введены метод Verify (в пользовательском интерфейсе) и метаморфное тестирование[1] (для разработчиков).
Экосистема проекта
В связи с тем, что проект пополнялся не только методами, но и новыми классами автоматов (в частности, «PDA» — стековые автоматы; «MFA» — автоматы с памятью), было решено расширить его экосистему средствами автоматического обновления, позволяющими быстро добавлять в интерфейс новый функционал. В модуль автотестирования помимо юнит-тестов были добавлены метаморфные тесты, проверяющие инвариантность свойств объектов относительно цепочек преобразований. В силу того, что некоторые классы автоматов (в частности, «MFA») имеют неразрешимое отношение эквивалентности, был разработан также фазз-модуль, осуществляющий приблизительную проверку равенства языков соответствующих распознавателей.
Сам конвертер написан на языках C++} (большая часть фронтенда и весь бэкенд) и Refal-5 (форматирующие скрипты для порождения \LaTeX-исходников). В связи с этим, отдельно стоит упомянуть экспериментальный проект Линтера для Refal-5, который служит цели улучшить дисциплину кода, ранее не контролировавшуюся никем, кроме самого разработчика, делающего коммиты, и находится на стадии встраивания в «CI» проекта.
Применение в исследованиях
Хотя изначально конвертер разрабатывался как чисто учебный проект, оказалось, что этот инструмент удобен и для теоретических исследований. В частности, посредством метода Verify удобно перепроверять утверждения на предмет неявных допущений, что показал анализ статьи [2], выявивший несколько неточностей в приведённых формулировках. Кроме того, методы анализа полугрупповых структур показали хорошую скорость и точность при выявлений «REDoS»-ситуаций в академических регулярных выражениях с перекрытиями в подвыражениях[3], для которых методы анализа, использующие самопересечения автоматов [4], работают слишком медленно, а фаззеры[5],[6] — ненадёжно. Последним применением конвертера на данный момент стало исследование бисимуляций в конечных автоматах с памятью посредством аппроксимаций классическими конечными автоматами[7]. Поставленная цель — сделать осязаемыми абстрактные концепции, используемые в современной теории формальных языков, — оказалась полезна не только для сдачи зачётов, но и для испытания новых гипотез.
Примечания и ссылки
- ↑ T. Y. Chen, S. C. Cheung, S. M. Yiu: Metamorphic testing: A new approach for generating next test cases // TR HKUST-CS98-01, Department of Computer Science, The Hong Kong University of Science and Technology, Hong Kong, 1998.
- ↑ C. Allauzen, M. Mohri: A Unified Construction of the Glushkov, Follow, and Antimirov Automata // TR2006-880, Courant Institute of Mathematical Sciences, 2006.
- ↑ A. N. Nepeivoda, Yu. A. Belikova, K. K. Shevchenko, M. R. Teriukha, D. P. Knyazihin, A. D. Delman, A. S. Terentyeva REDoS detection in ``Domino regular expressions by Ambiguity Analysis // Труды ИСП РАН 35(3), 109—124, 2023.
- ↑ N. Weideman, B. van der Merwe, M. Berglund, B. W. Watson:{Analyzing Matching Time Behavior of Backtracking Regular Expression Matchers by Using Ambiguity of {NFA}} //Proc. of Implementation and Application of Automata - 21st International Conference, {Lecture Notes in Computer Science}, 9705, p.322—334, 2016.
- ↑ Y. Shen, Y. Jiang, C. Xu, P. Yu, X. Ma, J. Lu: {Re{S}cue: Crafting Regular Expression DoS Attacks} // Proceedings of the 33rd ACM/IEEE International Conference on Automated Software Engineering, 225—235, 2018.
- ↑ Y. Liu, M. Zhang, W. Meng: {Revealer: Detecting and Exploiting Regular Expression Denial-of-Service Vulnerabilities} // Proceedings of the 2021 IEEE Symposium on Security and Privacy (SP), 1468—1484, 2021.
- ↑ A. N. Nepeivoda, A. D. Delman, A. S. Terentyeva Bisimulations in Memory Finite Automata // SYRCoSE 2024 Proceedings, 2024.