Свободные библиотеки в вычислительных задачах (Пётр Демин, OSEDUCONF-2016)
Материал из 0x1.tv
Содержание
Аннотация
- Докладчик
- Пётр Демин
Представлен опыт совместного использования компиляторов g++, gfortran и свободных математических библиотек для решения вычислительных задач. Особое внимание уделено решению вычислительных задач высокой точности. Рассмотрены возможности библиотек mpfr и c-xsc. Также представлены программные средства, позволяющие использовать графические возможности gnuplot.
Видео
Посмотрели доклад? Понравился? Напишите комментарий! Не согласны? Тем более напишите.
Слайды
Тезисы
При решении вычислительных задач основными языками программирования, позволяющими разрабатывать быстродействующие приложения являются С(С++) и Фортран.
Кроме стандартных средств языков программирования, в этих языках реализованы современные технологии параллельного программирования. Это позволяет использовать С и Фортран не только для решения задач на локальном персональном компьютере, но и при реализации задач на вычислительных кластерах.
В современных свободных компиляторах (gcc, g++, gfortran) реализованы все возможности современных языков С и Фортран. Компиляторы gcc, gfortran используются на всех современных кластерах наряду с компиляторами Intel. При решении вычислительных задач пользователь может столкнуться с несколькими проблемами:
- разработка и реализация высокоэффективных алгоритмов вычислительной математики;
- достижение достаточной точности вычислений;
- кросс-платформная реализация графического вывода результатов.
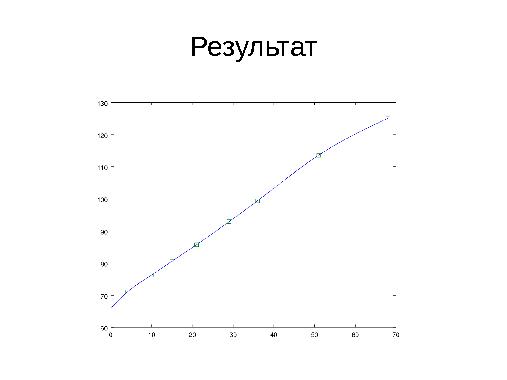
Имеет смысл использовать свободную научную библиотеку языка С GSL[1] при реализации алгоритмов вычислительной математики.
Библиотека позволяет решать:
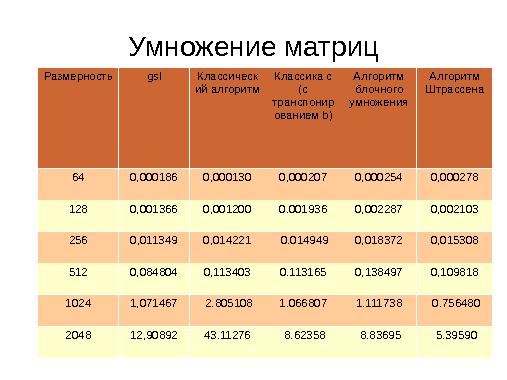
- некоторые задачи линейной алгебры (арифметические операции с матрицами (векторами) и поэлементное произведение, LU- и QR-разложение, нахождение собственных чисел и векторов);
- задачи локальной оптимизации (метод золотого сечения, метод Брента одномерной оптимизации и градиентные методы многомерной оптимизации Флетчера-Ривса, Полак-Райбьера и др.);
- задачи статистики (генерация и работа со случайными и квазислучайными последовательностями, нормальное распределение, распределение Пуассона и др);
- задачи численного интегрирования (в основе метод Гаусса-Кронрода с различным количеством точек, есть алгоритм с исключением особых точек, функция вычисления интеграла для колебательных функций, функция вычисления интеграла Фурье и др.);
- задачи с комплексными числами(арифметические операции, модуль, аргумент, поиск сопряженного, обратного, противоположного по знаку, возведение в степень, вычисление тригонометрических функций от комплексного числа и др);
- производить сортировку(пирамидальная сортировка) элементов массива (вектора).
Библиотека GSL предоставляет свой интерфейс для доступа к базовой библиотеке векторных и матричных операций blas. Существует интерфейс для использования библиотеки при написании программ на Фортране.
Довольно сложной проблемой при решении инженерных и математических задач является проблема точности вычислений. Встроенные в язык типы данных не позволяют гарантировать правильность вычислений при арифметических операциях с числами разных порядков.
На сегодняшний день существует несколько подходов для решения этой проблемы.
Авторами рассмотрены два подхода:
- использование интервального анализа для вычислений, существует несколько библиотек на С(С++) для реализации интервального анализа [2][3], одной из них является C-XSC. Библиотека имеет открытый исходный код. Имеет возможность работы с комплексными числами, матрицами и векторами. Также имеет ряд типов данных с префиксом l_, реализующих вычисления с повышенной точностью в интервалах. Имеется возможность распараллеливания некоторых функций с помощью OpenMP.
- использование вещественных чисел произвольной точности — (MPFR) — библиотеки языков С и С++, основанные на GMP. Поддерживает стандарт IEEE-754 для арифметических операций с числами с плавающей точкой. Позволяет инициализировать переменные с большой точностью, производить с ними арифметические операции, возводить их в степень, находить корень, вычислять логарифм и экспоненту, а также тригонометрические функции и константы. За счет возможности выбора количества бит, отводимое на хранение переменной, можно регулировать точность вычислений.
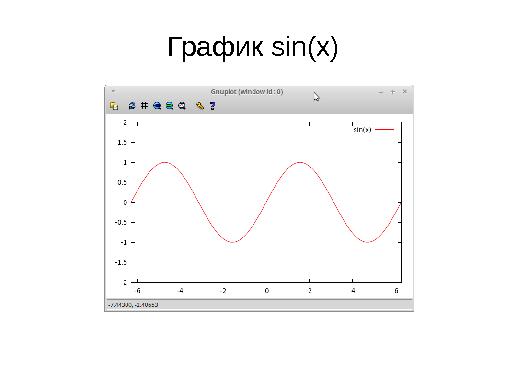
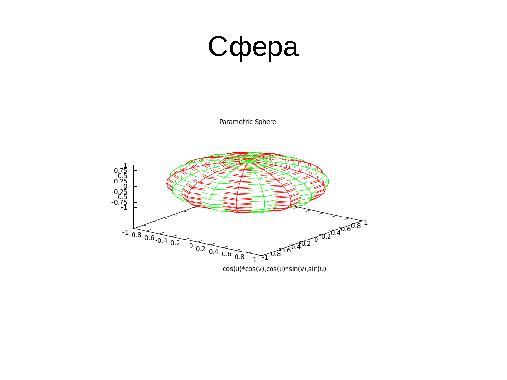
Одной из проблем при написании вычислительных консольных приложений на С(С++) и Фортране является вывод графиков с результатами работы программы. Для решения этой проблемы предлагается использовать возможности программы GNUPlot. Для этого необходим интерфейс между gfortran, g++, gcc и GNUPlot. В качестве интерфейса между Фортраном и GNUPlot можно предложить gnufor2, а между С и Gnuplot — gnuplot-cpp.
Примечания и отзывы
- ↑ GNU Scientific Library — http://www.gnu.org/software/gsl/
- ↑ Кулиш У., Рац Д., Хаммер Р., Хокс М. Достоверные вычисления. Базовые численные методы. — Москва-Ижевск: РХД, 2005. — 496с.
- ↑ Шарый С. П. Конечномерный интервальный анализ. — URL: http://www.nsc.ru/interval/Library/InteBooks/SharyBook.pdf
Plays:65 Comments:0