О необходимых знаниях и умениях для программистов суперкомпьютеров (Николай Непейвода, OSEDUCONF-2014) — различия между версиями

Версия 11:27, 15 февраля 2014

Содержание

1 Аннотация
2 Видео
3 Слайды
4 Примечания и отзывы

Аннотация

Докладчик: Николай Непейвода

Суперкомпьютеры высшего уровня в последние годы представляют собой быстро изменяющиеся сложные структуры, часто построенные на базе разнородных блоков. Это связано с тем, что они подошли к трём барьерам: скорость света, выделение тепла (предел Ландауэра) и предел Чейтина (предел сложности конструкций, которые может понять человек).
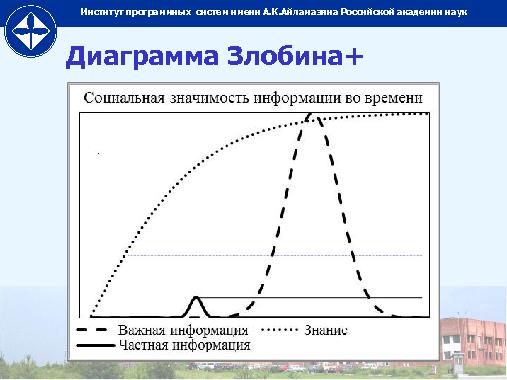
Казалось бы, последний предел самый невинный. Но, как отмечают многие, именно он сейчас стал определяющим в очень многих случаях. Появился термин «агрессивное невежество» программистов, которое приводит к тому, что программа оказывается полностью неадекватна системе на которой она исполняется.
Параллельные алгоритмы с самого начала строятся по другим законам, чем последовательные. Для их создания нужно логическое мышление, а логика как наука практически выброшена из учебных программ в России. «Математическая логика», под которой понимают классическую и в которой полностью опущен как неформализуемый раздел, посвящённый взаимосвязям формального и содержательного, лишь ещё более отупляет. Философская логика не лучше. А давать науку в комплексе не хватает ни часов, ни сил, ни методических разработок.
Логически созданная программа с самого начала максимально совместна (незаслуженно забытый термин из Алгола-68), что означает возможность легко уложить на любую подходящую для неё архитектуру. Это даёт отнюдь не оптимальное для конкретной аппаратуры решение, но на порядок лучше того, которое получается «распараллеливанием» изначально последовательной программы. Далее уже нужно одновременно и в комплексе видеть как алгоритм, так и ресурсные требования, что требует более высокого уровня знаний и умений.
Разные архитектуры суперкомпьютеров требуют для получения решения выше среднего различных неклассических логик. Это дополнительная объективная трудность: человек, который, преодолев недостатки образования, вошёл в одну из архитектур (например, в матрично-конвейерную), теряется, когда надо программировать, скажем, на ассоциативном процессоре обработки данных. Здесь нужен опыт преобразования математических структур (алгебраические концепции). Ситуация ещё обостряется в связи с перспективой перехода к алгебраическим процессорам. Поэтому современный программист суперкомпьютеров, не знающий алгебры, может освоить максимум одну структуру и перестроить мозги под неё. При переходе на другую его ум полностью сломается. А в бурно развивающейся отрасли такое недопустимо.
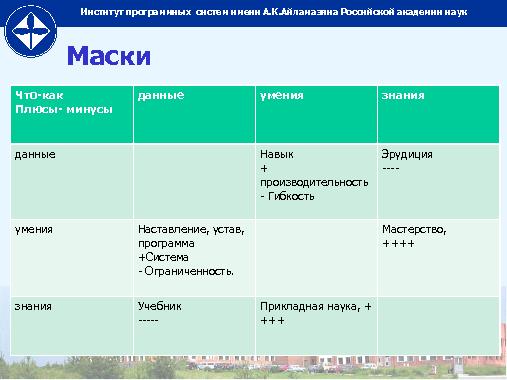
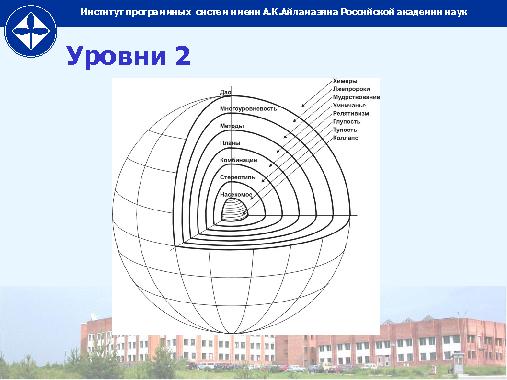
Но здесь ещё один важный аспект. Если теория и практика резко различаются по уровню, то начинаются нежелательные эффекты. Скажем, математический идиотизм, когда математика развита до третьего уровня (преобразования структур функций над объектами), а практика на нулевом. Но ещё хуже случай, когда практика на первом. Тогда математик самоуверенно выдаёт практические рекомендации отрицательной ценности. А вот если практика у него на втором (хотя бы освоение на дилетантском уровне всей системы стилей программирования), рекомендации становятся адекватными, он может посоветовать программисту, как перестроить структуры подновую архитектуру компьютеров. Аналогично, если теория на втором, а программирование на третьем, то программист сможет внятно поставить вопрос аналитику, подобрать адекватный инструмент и увидеть взаимосвязь программных структур и ресурсов в данной конкретной безумной архитектуре сверхпродвинутого суперкомпьютера.
Поэтому я полностью согласен с предложением С. М. Абрамова: суперкомпьютерная отрасль требует обучения студентов с самого начала по совершенно другим программам, чем обычные информати- ки. Мышление на уровне конкретных моделей неизбежно приводит к агрессивному невежеству в данной области. Нужно мышление по крайней мере на уровень выше (метамодели). На самом деле адекватно области мышление на уровне преобразований метамоделей. И очень важно здесь сбалансировать теоретические и практическое вопросы (в теории овладеть преобразованиями структур, а не фиксированной структурой чисел и их конкретных преобразований; в практике — концепциями и преобразованиями из одной формы в другую, а не отдельным «автоматом Калашникова»). В теории — логика и математика на базе алгебры, на практике — СПО.