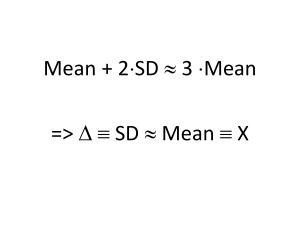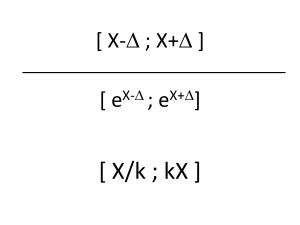Пуассоновое горение сроков (Андрей Бибичев, AgileDays-2011) — различия между версиями
Материал из 0x1.tv
StasFomin (обсуждение | вклад) (Batch edit: replace PCRE (\n\n)+(\n) with \2) |
StasFomin (обсуждение | вклад) |
||
== Презентация== <html><div style="width:595px" id="__ss_7462530"> <strong style="display:block;margin:12px 0 4px"><a href="http://www.slideshare.net/biBIGine/puasson-burning" title="Puasson burning" target="_blank">Puasson burning</a></strong> <iframe src="http://www.slideshare.net/slideshow/embed_code/7462530?rel=0" width="595" height="497" frameborder="0" marginwidth="0" marginheight="0" scrolling="no"></iframe> <div style="padding:5px 0 12px"> View more <a href="http://www.slideshare.net/" target="_blank">presentations</a> from <a href="http://www.slideshare.net/biBIGine" target="_blank">Andrey Bibichev</a> </div> </div> </html>* http://www.slideshare.net/biBIGine [[File:Пуассоновое горение сроков (Андрей Бибичев, AgileDays-2011).pdf|page=-|300px]] == Примечания и отзывы == | |||
Версия 11:54, 29 февраля 2024
Содержание
Аннотация
- Докладчик
- Андрей Бибичев
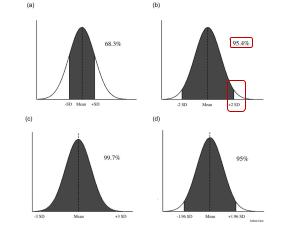
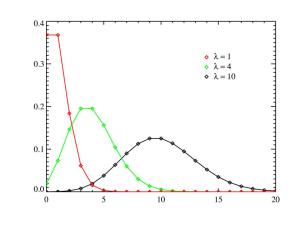
Когда мы говорим о какой-либо неопределенности, то чаще всего представляем гауссовское распределение:
- Какова трудоемкость этой задачи?
- Столько-то плюс/минус столько-то.
- А распределение?
- Гауссовское, конечно же!
Этот посыл можно встретить во многих хороших и в остальных аспектах замечательных работах на тему планирования и прогнозирования сроков.
Но он в корне неверен!
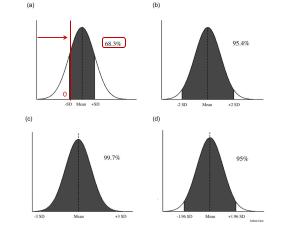
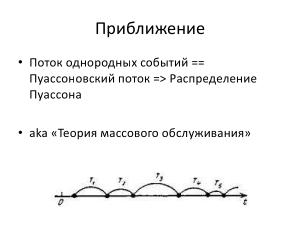
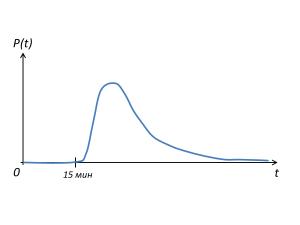
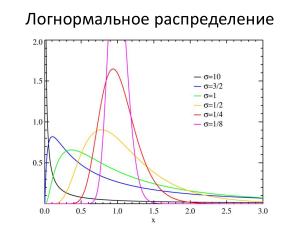
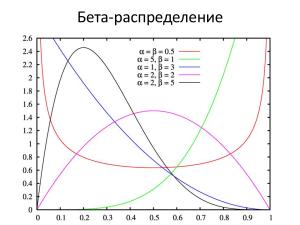
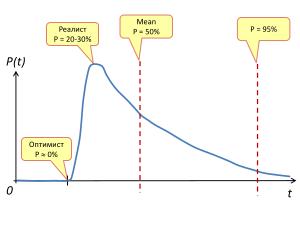
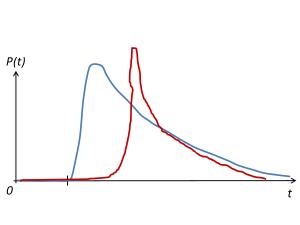
В докладе даются причины, по которым гауссовское распределение не подходит, и рассматривается распределение вероятности, значительно лучше подходящее для оценки трудоемкости и сроков. На основе этой несложной математики можно сделать простые, но весьма полезные в практическом плане выводы:
- почему разница между наиболее вероятным и гарантированным значениями примерно в 2-3 раза (сравните со своими эмпирическими коэффициентами и фокус-факторами!);
- почему чудес не бывает и в подавляющем большинстве случаев опаздываем со сроками, а не опережаем их (ведь гаусс нам сулит одинаковую вероятность как опоздать, так и сделать быстрее);
- какое отношение планирование имеет к теории массового обслуживания.
В докладе содержится чуть-чуть математики, которая не должна успеть сильно наскучить за 10 минут.
Видео
Посмотрели доклад? Понравился? Напишите комментарий! Не согласны? Тем более напишите.
Презентация
Примечания и отзывы
Plays:5842 Comments:1