Об эффективной реализации разрывного метода Галеркина применительно к решению двумерных задач газовой динамики на неструктурированных сетках (Виктория Корчагова, ISPRASOPEN-2018) — различия между версиями

;{{SpeakerInfo}}: {{Speaker|Виктория Корчагова}}
<blockquote>
Доклад посвящен способам ускорения вычислений при решении двумерных задач газовой динамики разрывным методом Галеркина на неструктурированных сетках. Ускорение может быть достигнуто как за счет выбора оптимальных с точки зрения временных затрат алгоритмов построения итоговой численной схемы, так и с помощью распараллеливания вычислений. 

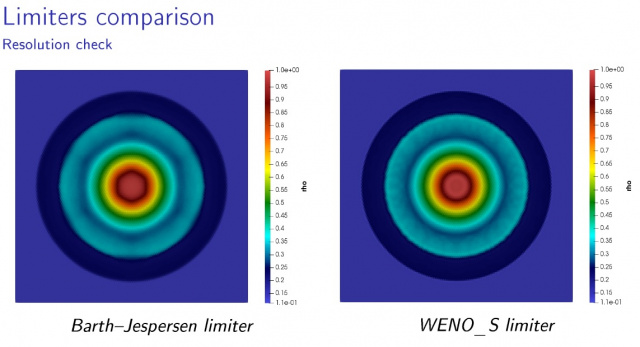
Реализован прототип программного комплекса на языке С++, в рамках которого рассматриваются различные способы решения системы ОДУ (методы Рунге—Кутты и Адамса), расчета численных потоков (LF, HLL, HLLC), монотонизации решения (лимитеры на основе технологии WENO и на основе локального принципа максимума). 

Рассмотрены параллельные реализации прототипа с использованием технологий OpenMP и MPI. Проведено сравнение результатов, полученных на ряде тестовых задач.
</blockquote>

{{VideoSection}}
{{vimeoembed|298786152|800|450}}
{{youtubelink|}}{{letscomment}}

{{SlidesSection}}
[[File:Об эффективной реализации разрывного метода Галеркина решения двумерных задач газовой динамики на неструктурированных сетках.pdf|left|page=-|300px]]

{{----}}
[[File:{{#setmainimage:Об эффективной реализации разрывного метода Галеркина решения двумерных задач газовой динамики на неструктурированных сетках!.jpg}}|center|640px]]