Wave Attractors (Leo Maas, ISPRASOPEN-2018) — различия между версиями

Версия 08:02, 21 декабря 2018

Speaker: Leo Maas

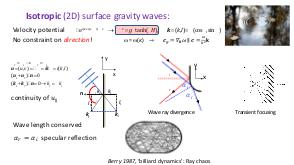
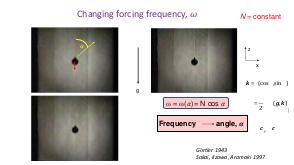
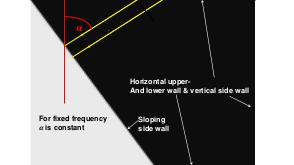
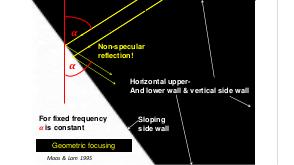
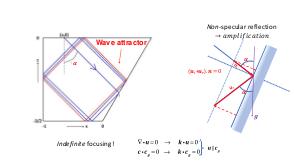
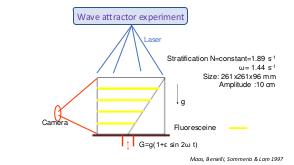
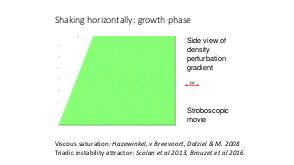
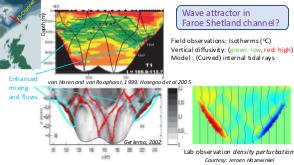
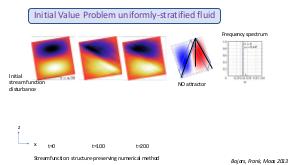
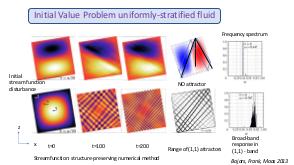
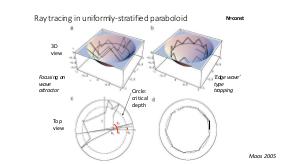
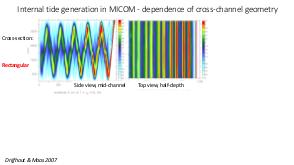
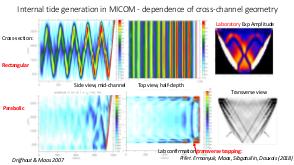
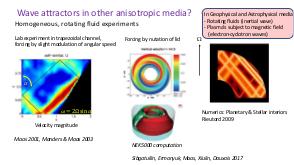
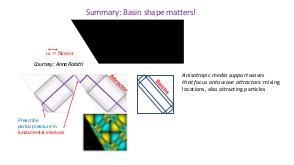
В теории динамических систем аттрактором является подмножество фазового пространства, к которому стремиться система независимо от начальных условий. В геофизических и астрофизических приложениях вращение и плотностная стратификация создают анизотропное состояние равновесия. Возмущения этих состояний равновесия проявляются в виде внутренних и инерционных волн. После отражения от наклонных по отношению к силе гравитации или направлению вращения границ, внутренние волны фокусируются и устремляются к подмножеству физического пространства, названному волновыми аттракторами.
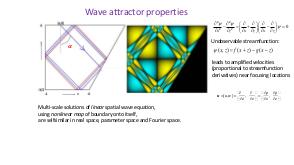
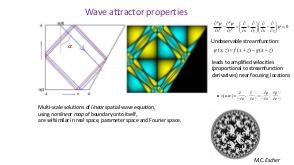
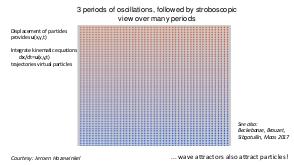
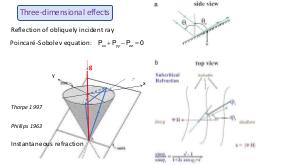
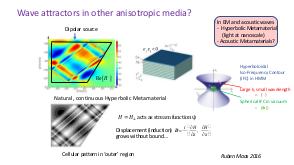
Теория и эксперимент позволяют прояснить природу и повсеместное присутствие волновых аттракторов, которые оказываются свойственными любой анизотропной волновой системе. Описана уникальная спектральная эволюция, определенная формой начальных возмущений. В то время как возмущения невязкой стратифицированной жидкости определяются линейным (пространственно гиперболическим) уравнением Пуанкаре-Соболева, в областях нетривиальной формы с нарушенной симметрией, волновые поля получаются применением нелинейного, диссипативного отображения границы в себя. Многие свойства, которые обычно ассоциируются с нелинейной динамикой (автомодельный спектр, автомодельные волновые поля, функция Вейерштрасса, дьявольская лестница, языки Арнольда) обнаруживаются в строго линейной постановке. Перефразируя определение Симона Стевина (1548—1620) «поразительное, но при этом не чудо» («wonder, not miracle»), можно описать подобную волновую систему как «линейную, но при этом нелинейную» (linear, yet nonlinear).