Свободные библиотеки интервальных вычислений при подготовке бакалавров и магистров направления «Математика и компьютерные науки» в Кубанском государственном университете (Станислав Гончаров, OSEDUCONF-2022) — различия между версиями

Материал из 0x1.tv

 
Одним из средств повышения достоверности компьютерных вычислений является интервальный анализ. В Кубанском
Государственном Университете изучение интервальных вычислений входит в программу подготовки бакалавров и магистров
направления «Математика и компьютерные науки». Бакалавры направления подготовки 02.03.01 «Математика и компьютерные
науки» (направленность подготовки «Вычислительные, программные, информационные системы и компьютерные технологии» )
знакомятся с интервальным анализом в курсе «Современные методы обработки числовых данных». Магистранты (направление
подготовки 02.04.01 Математика и компьютерные науки, направленность  —  Вычислительная математика) продолжают изучение
интервальных вычислений в рамках курса «Компьютерные технологии в науке и образовании».

На лабораторных работах используются следующие свободные программные средства интервальных вычислений<ref name="d1">Интервальный анализ и его приложения. Программное обеспечение и языки программирования. url:
[http://www.nsc.ru/interval/?page=Programing]</ref>:
# ; ([https://sourceforge.net/p/octave/interval/ci/]\\[default/tree/])  — Interval]:  пакет интервальных вычислений для Octave.
# ;[https://github.com/boostorg/interval Boost interval]: ([https://github.com/boostorg/interval])  —  библиотека интервалов на C++.
# ;[https://github.com/boostorg/interval Libieeep1788]: ([https://github.com/boostorg/interval])  —  библиотека интервалов, реализующая интервальную арифметику стандарта IEEE 1788.


В бакалавриате студенты в курсе «Современные методы обработки числовых данных» решают стандартные задачи, связанные с
высокоточными вычислениями, а также несложные задачи интервального анализа (найти корни нелинейного уравнения, задачи
линейной алгебры). Для решения подобных задач большинство студентов пользуется пакетом интервальных вычислений в
Octave.

В рамках лабораторных работ при изучении интервальных вычислений магистрантам могут быть предложены задачи, имеющие
реальное прикладное инженерное значение. Например, 


* Нестационарная задача теплопроводности<ref name="d2">Ерёмин&nbsp;А.&nbsp;В., Кудинов&nbsp;И.&nbsp;В. Об одном методе решения нестационарных задач теплопроводности Вестник Самарского государственного технического университета. Серия: Технические науки. 2012. № 2 (34). С. 158—164.</ref>
<latex>
\begin{gather*}
\frac{\partial t(x,\tau )}{\partial \tau }=a\frac{\partial ^2t(x,\tau )}{\partial x^2};\\
(\tau >0);0\le x\le \delta;\\
t(x,0)=t_0;\\
\frac{\partial t(0,\tau )}{\partial x}=0;\\
t(\delta ,\tau )=t_{\tilde  n\grave o}.
\end{gather*}
</latex>
*  Задача Ван-Дер-Поля<ref name="d3">Хайрер&nbsp;Э., Ваннер&nbsp;Г. Решение обыкновенных дифференциальных уравнений. Жёсткие и дифференциально-алгебраические задачи: пер. с англ. М. : Мир, 1999. 685&nbsp;с.</ref>
<latex>
\begin{gather*}
	\frac{dy_1}{dt}=y_2\\
\frac{dy_2}{dt}=\mu (1-y_1^2)y_2-y_1;\\
y_1(0)=2;\\
y_2(0)=0;\\
0\le t\le T
\end{gather*}
</latex>
где <m>\mu</m>  —  коэффициент жёсткости. Причём, чем больше значение µ, тем более жёсткой становится задача.
*  Прямая и обратная геодезические задачи<ref name="d4">Ботнев&nbsp;В.&nbsp;А., Устинов&nbsp;С.&nbsp;М. Методы решения прямой и обратной геодезических задач с высокой точностью Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Информатика. Телекоммуникации. Управление. 2014. № 3 (198). С. 49—58.</ref>

Прямая задача: по заданной широте <m>\varphi </m>1 и долготе <m>\lambda </m>1 первой точки требуется найти
географические координаты <m>\varphi </m>2 и <m>\lambda </m>2 второй точки, если известны начальный азимут <m>\alpha</m> и расстояние
D между этими точками см рисунок:

[[File:2023-oseduconf-4-img001.png|center|640px]]

*  Жёсткое дифференциальное уравнение первого порядка<ref name="d5">Бандурин&nbsp;Н.&nbsp;Г.Численное решение жёстких нелинейных задач. Вестник Волгоградского государственного архитектурно-строительного университета. Серия: Строительство и архитектура. 2010. № 17 (36). С. 17—23.</ref>
<latex>
	\begin{gather*}
		\varepsilon{}y'+(1+t)y-t-1=0;\\
y(0)=0; t\in (0,2)
	\end{gather*}
#</latex>
*  Дифференциальное уравнение [5]<ref name="d5"/>
<latex></ref>
\begin{gather*}
y'+y\tan (t)-100t^2\cos (t)^2=0;\\
y(0)=0; t\in (0,\frac{\pi } 2)
\end{gather*}
# </latex>
* Краевая задача [5]<ref name="d5"/>
<latex></ref>
\begin{gather*}
\varepsilon y''+xy'+y=0;\\
	y(0)=1;\\
	y(1)=\exp (-0.5\varepsilon );\\
\varepsilon =1/300
\end{gather*}
</latex>

Количество часов, отводимых на изучение интервальных задач в магистратуре в рамках курса «Компьютерные технологии в науке и
образовании» невелико. Чтобы все магистранты смогли справится с реальными задачами, была разработана библиотека решения
задач методом интервальных вычислений. Библиотека использует класс интервалов библиотеки boost interval и свободные

Версия 17:27, 25 февраля 2024

Докладчик
Станислав Гончаров

Изучение интервальных вычислений входит в программу подготовки бакалавров и магистров направления «Математика и компьютерные науки» в Кубанском Государственном Университете. Бакалавры знакомятся с интервальным анализом в курсе «Современные методы обработки числовых данных». Магистранты продолжают изучение интервальных вычислений в рамках курса «Компьютерные технологии в науке и образовании».

Используя свободные библиотеки интервальных вычислений, авторы разработали библиотеку решения инженерных задач, которая используется в учебном процессе.

Видео

Презентация

300px

Thesis

Увеличение вычислительных мощностей современных компьютеров предоставляет возможность решать сложные научные и инженерные задачи, нередко требующие большого количества операций с плавающей точкой. Решение задач, описывающих реальные высокоточные процессы — есть хороший фундамент подготовки будущих инженеров и программистов.

Одним из средств повышения достоверности компьютерных вычислений является интервальный анализ. В Кубанском Государственном Университете изучение интервальных вычислений входит в программу подготовки бакалавров и магистров направления «Математика и компьютерные науки». Бакалавры направления подготовки 02.03.01 «Математика и компьютерные науки» (направленность подготовки «Вычислительные, программные, информационные системы и компьютерные технологии» ) знакомятся с интервальным анализом в курсе «Современные методы обработки числовых данных». Магистранты (направление подготовки 02.04.01 Математика и компьютерные науки, направленность — Вычислительная математика) продолжают изучение интервальных вычислений в рамках курса «Компьютерные технологии в науке и образовании».

На лабораторных работах используются следующие свободные программные средства интервальных вычислений[1]:

Interval
пакет интервальных вычислений для Octave.
Boost interval
библиотека интервалов на C++.
Libieeep1788
библиотека интервалов, реализующая интервальную арифметику стандарта IEEE 1788.


В бакалавриате студенты в курсе «Современные методы обработки числовых данных» решают стандартные задачи, связанные с высокоточными вычислениями, а также несложные задачи интервального анализа (найти корни нелинейного уравнения, задачи линейной алгебры). Для решения подобных задач большинство студентов пользуется пакетом интервальных вычислений в Octave.

В рамках лабораторных работ при изучении интервальных вычислений магистрантам могут быть предложены задачи, имеющие реальное прикладное инженерное значение. Например,


  • Нестационарная задача теплопроводности[2]

  • Задача Ван-Дер-Поля[3]

где — коэффициент жёсткости. Причём, чем больше значение µ, тем более жёсткой становится задача.

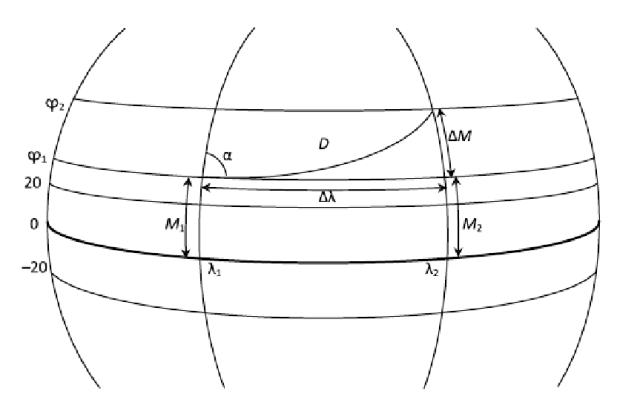
  • Прямая и обратная геодезические задачи[4]

Прямая задача: по заданной широте 1 и долготе 1 первой точки требуется найти географические координаты 2 и 2 второй точки, если известны начальный азимут и расстояние D между этими точками см рисунок:

2023-oseduconf-4-img001.png
  • Жёсткое дифференциальное уравнение первого порядка[5]

  • Дифференциальное уравнение[5]

  • Краевая задача[5]

Количество часов, отводимых на изучение интервальных задач в магистратуре в рамках курса «Компьютерные технологии в науке и образовании» невелико. Чтобы все магистранты смогли справится с реальными задачами, была разработана библиотека решения задач методом интервальных вычислений. Библиотека использует класс интервалов библиотеки boost interval и свободные компиляторы семейства gcc. В состав библиотеки входят функции, реализующие:


  1. Простейшие матричные операции (сложение, вычитание, умножение матрицы на число, произведение матриц, транспонирование матриц, вычисление обратной матрицы), вычисление определителя матрицы.
  2. Алгоритмы решения систем линейных алгебраических уравнений (метод Гауса, Жордана-Гауса, LU-разложение, QR-разложение).
  3. Алгоритмы решения нелинейных уравнений и систем.
  4. Алгоритмы решения дифференциальных уравнений первого и второго порядков.

Набор этих инструментов позволит использовать библиотеку в решении моделей инженерных задач в образовательном процессе.

В результате изучения интервальных вычислений в рамках дисциплин «Современные методы обработки числовых данных» и «Компьютерные технологии в науке и образовании» студенты получат не только теоретические знания, но и смогут применить эти знания на практике при решении прикладных инженерных задач.

Работа выполнена при финансовой поддержке Кубанского научного фонда в рамках научного проекта № ППН-21.1/10 «Цифровая дидактика для предметного обучения, воспитательной работы учащихся и профессиональной подготовки учителей».


640px

Примечания и ссылки

  1. ↑ Интервальный анализ и его приложения. Программное обеспечение и языки программирования. url: [1]
  2. ↑ Ерёмин А. В., Кудинов И. В. Об одном методе решения нестационарных задач теплопроводности Вестник Самарского государственного технического университета. Серия: Технические науки. 2012. № 2 (34). С. 158—164.
  3. ↑ Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жёсткие и дифференциально-алгебраические задачи: пер. с англ. М. : Мир, 1999. 685 с.
  4. ↑ Ботнев В. А., Устинов С. М. Методы решения прямой и обратной геодезических задач с высокой точностью Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Информатика. Телекоммуникации. Управление. 2014. № 3 (198). С. 49—58.
  5. ↑ 5,0 5,1 5,2 Бандурин Н. Г.Численное решение жёстких нелинейных задач. Вестник Волгоградского государственного архитектурно-строительного университета. Серия: Строительство и архитектура. 2010. № 17 (36). С. 17—23.
Источник — «https://0x1.tv/index.php?title=Свободные_библиотеки_интервальных_вычислений_при_подготовке_бакалавров_и_магистров_направления_«Математика_и_компьютерные_науки»_в_Кубанском_государственном_университете_(Станислав_Гончаров,_OSEDUCONF-2022)&oldid=189402»