Свободные библиотеки интервальных вычислений при подготовке бакалавров и магистров направления «Математика и компьютерные науки» в Кубанском государственном университете (Станислав Гончаров, OSEDUCONF-2022) — различия между версиями

;{{SpeakerInfo}}: {{Speaker|Екатерина ЛапшинаСтанислав Гончаров}}
<blockquote>
Рассмотрены варианты разработки программного кода с использованием свободного программного обеспечения, которое позволяет создать программный продукт с минимальным набором навыков через визуальные интерфейсы и конструкторы с помощью Low-code платформыИзучение интервальных вычислений входит в программу подготовки бакалавров и магистров направления «Математика и компьютерные науки» в Кубанском Государственном Университете. Бакалавры знакомятся с интервальным анализом в курсе «Современные методы обработки числовых данных». Магистранты продолжают изучение интервальных вычислений в рамках курса «Компьютерные технологии в науке и образовании». 

Используя свободные библиотеки интервальных вычислений, авторы
разработали библиотеку решения инженерных задач, которая используется в учебном процессе.
</blockquote>

{{VideoSection}}
{{vimeoembed|917654020|800|450}}
{{youtubelink|}}
|TRsttECsqzU}}
{{SlidesSection}}
[[File:Тенденции разработки программного обеспечения с использованием Low-code платформСвободные библиотеки интервальных вычислений при подготовке направления «Математика и компьютерные науки» (Екатерина Лапшина, OSEDUCONF-2022).pdf|left|page=-|300px]]

{{----}}

== Thesis ==
Low-code платформы разработки — это приложение, котороеУвеличение вычислительных мощностей современных компьютеров предоставляет графический пользовательский интерфейс для
программирования и, таким образом, разрабатывает код с большей скоростью и сокращает затраченные усилия с минимальным
количеством кодирования. 

Подобные платформы реализованы в том числе, как свободное программноевозможность решать сложные научные и
инженерные задачи, нередко требующие большого количества операций с плавающей точкой. Решение задач, описывающих
реальные высокоточные процессы  —  есть хороший фундамент подготовки будущих инженеров и программистов.

Одним из средств повышения достоверности компьютерных вычислений является интервальный анализ. В Кубанском
Государственном Университете изучение интервальных вычислений входит в программу подготовки бакалавров и магистров
направления «Математика и компьютерные науки». Бакалавры направления подготовки 02.03.01 «Математика и компьютерные
науки» (направленность подготовки «Вычислительные, программные, информационные системы и компьютерные технологии» )
знакомятся с интервальным анализом в курсе «Современные методы обработки числовых данных». Магистранты (направление
подготовки 02.04.01 Математика и компьютерные науки, направленность  —  Вычислительная математика) продолжают изучение
интервальных вычислений в рамках курса «Компьютерные технологии в науке и образовании».

На лабораторных работах используются следующие свободные программные средства интервальных вычислений(СПО)<ref name="d1">[https://www.hmong.press/wiki/Low-code_development_platform Платформа разработки low-code — определение]</ref>.

Такие среды разработки применяются для создания прикладного программного обеспечения через графический интерфейс
пользователя вместо стандартного программирования вручную. С помощью платформ Low-code возможно создание полностью
рабочего приложения, а в редких случаях  —  с использованием дополнительного кодирования. Данные среды разработки
также помогают сократить объём программирования, что позволяет ускорить создание приложений. Большим преимуществом
является то, что расширяется круг людей, которые могут внести свой вклад в разработку приложения. Low-code платформы
также могут снизить первоначальные затраты на настройку, обучение и обслуживание. 

Недавнее исследование бостонской компании Mendix показало, что спрос на разработчиков среди ИТ-специалистов достиг
апогея. Почти шесть из десяти (57%) говорят, что количество персонала, необходимого для разработки программного
обеспечения, увеличивается, а [https://www.reworked.co/information-management/whats-behind-the-explosion-of-low-code-and-no-code-applications/ стоимость разработки программного обеспечения растёт (61%)]. 

Также отметим, что в связи с растущими ожиданиями клиентов и изменением потребностей рынка после пандемии предприятия в разных отраслях всё
Интервальный анализ и его приложения. Программное обеспечение и языки программирования. url:
[http://www.nsc.ru/interval/?page=Programing]</ref>:
;[https://sourceforge.net/p/octave/interval/ci/default/tree/ Interval]:  пакет интервальных вычислений для Octave.
;[https://github.com/boostorg/interval Boost interval]:  библиотека интервалов на C++.
;[https://github.com/boostorg/interval Libieeep1788]: библиотека интервалов, реализующая интервальную арифметику стандарта IEEE 1788.


В бакалавриате студенты в курсе «Современные методы обработки числовых данных» решают стандартные задачи, связанные с
высокоточными вычислениями, а также несложные задачи интервального анализа (найти корни нелинейного уравнения, задачи
линейной алгебры). Для решения подобных задач большинство студентов пользуется пакетом интервальных вычислений в
Octave.

В рамках лабораторных работ при изучении интервальных вычислений магистрантам могут быть предложены задачи, имеющие
реальное прикладное инженерное значение. Например, 


* Нестационарная задача теплопроводности<ref name="d2">Ерёмин&nbsp;А.&nbsp;В., Кудинов&nbsp;И.&nbsp;В. Об одном методе решения нестационарных задач теплопроводности Вестник Самарского государственного технического университета. Серия: Технические науки. 2012. № 2 (34). С. 158—164.</ref>
<latex>
\begin{gather*}
\frac{\partial t(x,\tau )}{\partial \tau }=a\frac{\partial ^2t(x,\tau )}{\partial x^2};\\
(\tau >0);0\le x\le \delta;\\
t(x,0)=t_0;\\
\frac{\partial t(0,\tau )}{\partial x}=0;\\
t(\delta ,\tau )=t_{\tilde  n\grave o}.
\end{gather*}
</latex>
*  Задача Ван-Дер-Поля<ref name="d3">Хайрер&nbsp;Э., Ваннер&nbsp;Г. Решение обыкновенных дифференциальных уравнений. Жёсткие и дифференциально-алгебраические задачи: пер. с англ. М. : Мир, 1999. 685&nbsp;с.</ref>
<latex>
\begin{gather*}
	\frac{dy_1}{dt}=y_2\\
\frac{dy_2}{dt}=\mu (1-y_1^2)y_2-y_1;\\
y_1(0)=2;\\
y_2(0)=0;\\
0\le t\le T
\end{gather*}
</latex>
где <m>\mu</m>  —  коэффициент жёсткости. Причём, чем больше проявляют инициативу в создании цифрового контента для потребителей. Поэтому сегодня одним из актуальных решений
является работа с Low-code платформами.

Рассмотрим варианты Low-code платформ для различных целей.

* [https://nl-значение µ, тем более жёсткой становится задача.
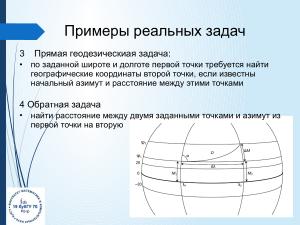
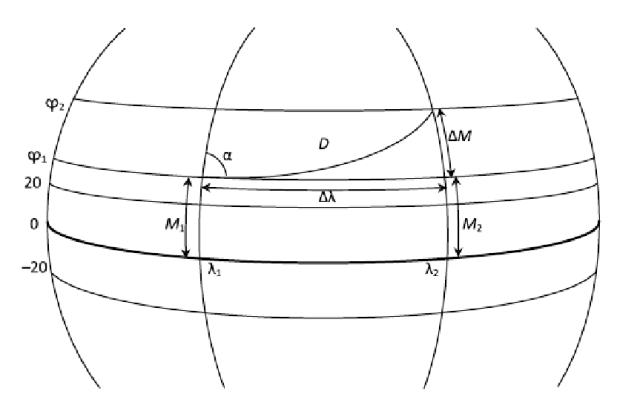
*  Прямая и обратная геодезические задачи<ref name="d4">Ботнев&nbsp;В.&nbsp;А., Устинов&nbsp;С.&nbsp;М. Методы решения прямой и обратной геодезических задач с высокой точностью Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Информатика. Телекоммуникации. Управление. 2014. № 3 (198). С. 49—58.</ref>

Прямая задача:.ru/nla-framework NL!A framework] — российский бесплатный low-code framework, позволяющий создавать полноценные бизнес-приложения. Модели, заложенные в кодогенератор NL!A framework, позволяют за считаные секунды создать полноценное рабочее бизнес-приложение;
* [https://www.outsystems.com/ OutSystem] — это надёжная и гибкая low-code платформа для разработки корпоративных мобильных и веб-приложений, которые разворачиваются в локальной или в гибридных средах;
* [https://soware.ru/products/mendix Mendix] — это бескодовая (no-code) программная платформа, предоставляющая инструменты для создания, тестирования,развёртывания и проверки программных приложений.


Помимо бесплатных версий популярных платформ, также существуют различные варианты Low-code СПО с открытым исходным
кодом, таких как Appsemble, Skyve, Baserow и другие. Наличие таких разнообразных платформ говорит о популярности данных
решений и их развитии.

Есть ряд других причин, по которым предприятиям следует рассматривать Low-code платформы:
#  Более быстрый выход на рынок;
#  Повышение удовлетворённости клиентов;
#  Снижение затрат на ИТ-инфраструктуру;
#  Более эффективное управление приложениями;
#  Лучшее управление ИТ;


Безусловно, подобные среды разработки — это панацея, а лишь вариант решения для создания программного продукта, поэтому
Low-code платформы имеют ряд минусов:
#  Сложность в выборе подходящего ресурса;
#  Ограничения в функционале;
#  Зависимость от платформы;


Рассматривая плюсы и минусы Low-code платформ, можно сделать вывод, что они отлично подходят для быстрого создания
небольших проектов и увеличениязаданной широте <m>\varphi </m>1 и долготе <m>\lambda </m>1 первой точки требуется найти
географические координаты <m>\varphi </m>2 и <m>\lambda </m>2 второй точки, если известны начальный азимут <m>\alpha</m> и расстояние
Dреализуемых решений. Они сокращают разрыв между пользователями и
разработчиками, что позволяет в короткий срок получить работающий прототип и сформировать видение будущей .
Также можно проследить стремительное развитие данного направления в целом и как СПО.

См  также: Лапшина Е.А., Симонов В.Л. Преимущества информационных систем с веб-интерфейсом // XIX Международная конференция
«Современныеэтими точками см рисунок:

[[File:2023-oseduconf-4-img001.png|center|640px]]

*  Жёсткое дифференциальное уравнение первого порядка<ref name="d5">Бандурин&nbsp;Н.&nbsp;Г.Численное решение жёстких нелинейных задач. Вестник Волгоградского государственного архитектурно-строительного университета. Серия: Строительство и архитектура. 2010. № 17 (36). С. 17—23.</ref>
<latex>
	\begin{gather*}
		\varepsilon{}y'+(1+t)y-t-1=0;\\
y(0)=0; t\in (0,2)
	\end{gather*}
</latex>
*  Дифференциальное уравнение<ref name="d5"/>
<latex>
\begin{gather*}
y'+y\tan (t)-100t^2\cos (t)^2=0;\\
y(0)=0; t\in (0,\frac{\pi } 2)
\end{gather*}
</latex>
* Краевая задача<ref name="d5"/>
<latex>
\begin{gather*}
\varepsilon y''+xy'+y=0;\\
	y(0)=1;\\
	y(1)=\exp (-0.5\varepsilon );\\
\varepsilon =1/300
\end{gather*}
</latex>

Количество часов, отводимых на изучение интервальных задач в магистратуре в рамках курса «Компьютерные технологии в науке и
образовании» невелико. Чтобы все магистранты смогли справится с реальными задачами, была разработана библиотека решения
задач методом интервальных вычислений. Библиотека использует класс интервалов библиотеки boost interval и свободные
компиляторы семейства gcc. В состав библиотеки входят функции, реализующие:


#  Простейшие матричные операции (сложение, вычитание, умножение матрицы на число, произведение матриц, транспонирование матриц, вычисление обратной матрицы), вычисление определителя матрицы.
#  Алгоритмы решения систем линейных алгебраических уравнений (метод Гауса, Жордана-Гауса, LU-разложение, QR-разложение).
#  Алгоритмы решения нелинейных уравнений и систем.
#  Алгоритмы решения дифференциальных уравнений первого и второго порядков.

Набор этих инструментов позволит использовать библиотеку в решении моделей инженерных задач в образовательном процессе.

В результате изучения интервальных вычислений в рамках дисциплин «Современные методы обработки числовых данных» и
«Компьютерные технологии в науке и образовании» студенты получат не только теоретические знания, но и смогут применить
эти знания на практике при решении прикладных инженерных задач.

<i>Работа выполнена при финансовой поддержке Кубанского научного фонда в рамках научного проекта № ППН-21.1/10
«Цифровая дидактика для предметного обучения, воспитательной работы учащихся и профессиональной подготовки учителей».</i>
технологии в образовании, науке и промышленности» 29—30 апреля 2021 года, г. Москва.

{{----}}
[[File:{{#setmainimage:Тенденции разработки программного обеспечения с использованием Low-code платформСвободные библиотеки интервальных вычислений при подготовке направления «Математика и компьютерные науки» (Екатерина Лапшина, OSEDUCONF-2022)!.jpg}}|center|640px]]
{{LinksSection}}
<!-- <blockquote>[©]</blockquote> -->

<references/>

[[Категория:OSEDUCONF-2022]]
[[Категория:Draft]]