Использование компиляторов языка Фортран при решении вычислительных задач (Вячеслав Стародумов, OSEDUCONF-2018) — различия между версиями
Материал из 0x1.tv
StasFomin (обсуждение | вклад) |
StasFomin (обсуждение | вклад) |
||
| (не показано 11 промежуточных версий этого же участника) | |||
;{{SpeakerInfo}}: {{Speaker|Вячеслав Стародумов}}
<blockquote>
Представлен обзор основных возможностей современных компиляторов (gfortran, ifort) языка Фортрана при решении вычислительных задач.
</blockquote>
{{VideoSection}}
{{vimeoembed|254114850|800|450}}
{{youtubelink|BE5GH2zFjDo}}{{letscomment}}
{{SlidesSection}}
[[File:Использование компиляторов языка Фортран при решении вычислительных задач (Вячеслав Стародумов, OSEDUCONF-2018).pdf|left|page=-|300px]]
{{----}}
== Thesis ==
<latex>
Фортран "---— первый язык программирования высокого уровня, ориентированный на решение вычислительных задач. Современный
Фортран в первую очередь ориентирован на высокоэффективные вычисления.
Среди основных нововведений Фортрана можно выделить:
\begin{itemize}
\item* поддержка длинных чисел (шестнадцатибайтные целые и вещественные тридцатидвухбайтные комплексные числа);
\item* динамические массивы переменной длины;
\item* все основные операции, процедуры и функции языка выполняются не только над скалярными величинами, но и над
массивами, матрицами, а также их фрагментами "---— секциями\footnote{<ref>Секция массива "---— часть массива, которая
определяется именем массива и границами изменения индексов (например, \Sys{<code>x(:,4)</code>, <code>y(1:15:3)}</code>).}</ref>;
\item* в современных компиляторах реализована конвейерная обработка операций и функций над массивами и секциями,
благодаря чему исполняемый код программ обработки массивов и матриц, генерируемый компиляторами Фортрана, является
самым быстрым;
\item* поддержка параллельных вычислений на уровне стандарта языка: параллельные циклы, комассивы;
\item* поддержка технологий параллельного программирования MPI, OpenMP;
\item* внедрение технологии автораспараллеливания в компиляторе ifort.
\end{itemize}
Многие экономические, инженерные и вычислительные задачи сводятся к задачам умножения матриц и решению систем линейных
алгебраических уравнений большой размерности. Рассмотрим, какие возможности предоставляют современные компиляторы для
решения этих задач.
При анализе быстродействия авторами использовались следующие компиляторы языка Фортран:
\begin{itemize}
\item* свободный компилятор gfortran (ver 7.2), поддерживающий большинство возможностей современных стандартов языка;
компилятор gfortran портирован в Windows;
\item* проприетарный компилятор компании Intel "---— ifort, входящий в состав комплекса проприетарных программ Intel
Parallel Studio; компилятор доступен для бесплатного использования в некоммерческих целях преподавателями, студентами и
научными работниками;
\item* компилятор pgfortran, входящий в состав PGI Edition, которыей поддерживает технологию CUDA; cсуществует версия
компиляторов семейства PGI "---— PGI Community Edition.
\end{itemize}
В очень многих вычислительных задачах необходимо выполнять матричные операции. Самой затратной матричной операцией
является операция умножение матриц\footnote{<ref>Частным случаем матричного умножения являются "---— умножение матрицы на
вектор и скалярное произведение векторов.}</ref>. Авторами была проанализирована эффективность умножения матриц на
современном Фортране. В Фортране присутствует встроенная подпрограмма умножения матриц <code>matmul</code>, в последней версии
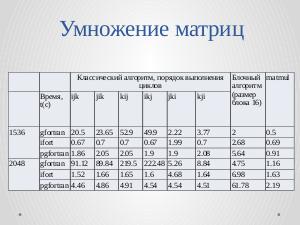
gfortran (gfortran-7) функция значительно оптимизирована. В таблице~\ref{aer-tbl00}Ниже приведены результаты времени выполнения программ,
реализующих классический и блочный алгоритмы умножения матриц и подпрограммы matmul.
<code>matmul</code>.
{| class="wikitable" style="font-size:85%; text-align:center;"
|+ '''Быстродействие программ (время, с), реализующих классический и блочный алгоритмы на Фортране с использованием свободных и проприетарных компиляторов'''
|-
! rowspan="2" |
! rowspan="2" | Компилятор
! colspan="6" | Классический алгоритм, порядок выполнения циклов
! rowspan="2" | Блочный алгоритм<br>(размер блока 16)
! rowspan="2" | matmul
|-
! ijk !! jik !! kij !! ikj !! jki !! kji
|-
| 1536 || gfortran || 20.5 || 23.65 || 52.9 || 49.9 || 2.22 || 3.77 || 2 || 0.5
|-
| || ifort || 0.67 || 0.7 || 0.7 || 0.67 || 1.99 || 0.7 || 2.68 || 0.69
|-
| || pgfortran || 1.86 || 2.05 || 2.05 || 1.9 || 1.9 || 2.08 || 5.64 || 0.91
|-
| 2048 || gfortran || 91.12 || 89.84 || 219.5 || 222.48 || 5.26 || 8.84 || 4.75 || 1.16
|-
| || ifort || 1.52 || 1.66 || 1.65 || 1.6 || 4.68 || 1.64 || 6.98 || 1.63
|-
| || pgfortran || 4.46 || 4.86 || 4.91 || 4.54 || 4.54 || 4.51 || 61.78 || 2.19
|}
<latex>
\begin{table}
\begin{center}
\tabcolsep=0.2em\scriptsize
\caption{\scriptsize Быстродействие программ (время, с), реализующих классический и блочный алгоритмы на Фортране с использованием свободных и проприетарных компиляторов}\label{aer-tbl00}
\begin{tabular}{|l|p{0.13\textwidth}|p{0.07\textwidth}|p{0.07\textwidth}|p{0.07\textwidth}|p{0.07\textwidth}|p{0.07\textwidth}|p{0.07\textwidth}|p{0.12\textwidth}|p{0.12\textwidth}|}\hline
& &\multicolumn{6}{p{0.42\textwidth}|}{Классический алгоритм, порядок выполнения циклов} &\multicolumn{1}{p{0.12\textwidth}|}{Блочный алгоритм (размер блока 16)} &\multicolumn{1}{p{0.12\textwidth}|}{matmul}
\\\hhline{--------~~}
&Время, t(c) &ijk &jik &kij &ikj &jki &kji & &\\\hline
1536 &gfortran &20.5 &23.65 &52.9 &49.9 &2.22 &3.77 &2 &0.5\\\hline
&ifort &0.67 &0.7 &0.7 &0.67 &1.99 &0.7 &2.68 &0.69\\\hhline{~---------}
&pgfortran &1.86 &2.05 &2.05 &1.9 &1.9 &2.08 &5.64 &0.91\\\hhline{~---------}
2048 &gfortran &91.12 &89.84 &219.5 &222.48 &5.26 &8.84 &4.75 &1.16\\\hline
&ifort &1.52 &1.66 &1.65 &1.6 &4.68 &1.64 &6.98 &1.63\\\hhline{~---------}
&pgfortran &4.46 &4.86 &4.91 &4.54 &4.54 &4.51 &61.78 &2.19\\\hline
\end{tabular}
\end{center}
\end{table}
</latex>
При использовании проприетарных компиляторов, не важно в каком порядке записывать циклы в коде программ умножения
матриц. Компиляторы <tt>ifort</tt>, <tt>pgfortran</tt>, достаточно хорошо оптимизируют исходный код. При использовании <tt>gfortran
</tt> программист должен аккуратно писать код, записывая циклы в оптимальном для данного языка порядке. Подпрограмма
умножения матриц, сформированная с помощью процедуры <tt>matmul</tt> и скомпилированная с помощью <tt>gfortran</tt> оказалась быстрее
любого другого кода (даже быстрее блочного алгоритма и алгоритма Штрассена). Авторы сравнивали быстродействие программ
умножения, написанных с использованием классических циклов на С и Фортране. Программы на Фортране работают на 10-–12\%
быстрее. Использование <tt>matmul</tt> и свободного компилятора позволяет ускорить работу программы ещё в несколько раз. Поэтому
именно <tt>matmul</tt> и новый компилятор <tt>gfortran-7</tt> следует использовать для решения задач, сводящихся к умножению матриц.
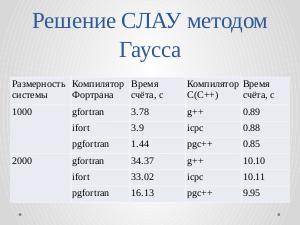
Одной из тестовых задач анализа быстродействия является метод Гаусса решения СЛАУ. Было проведено сравнение
быстродействие программ на С и Фортране (см табл. 2)
Таблица 2. .
{| class="wikitable" style="font-size:85%; text-align:center;"
|+ '''Время счёта программ на Фортране и С(С++) решения СЛАУ методом Гаусса.'''
|-
! Размерность системы !! Компилятор Фортрана !! Время счёта, с !! Компилятор С(С++) !! Время счёта, с
|-
| 1000 || gfortran || 3.78 || g++ || 0.89
|-
| || ifort || 3.9 || icpc || 0.88
|-
| || pgfortran || 1.44 || pgc++ || 0.85
|-
| 2000 || gfortran || 34.37 || g++ || 10.10
|-
| || ifort || 33.02 || icpc || 10.11
|-
| || pgfortran || 16.13 || pgc++ || 9.95
|}
<latex>
\begin{table}
\begin{center}
\tabcolsep=0.2em\scriptsize
\caption{\scriptsize Время счёта программ на Фортране и С(С++) решения СЛАУ методом Гаусса.}\label{aer-tbl01}
\begin{tabular}{|p{0.15\textwidth}|p{0.21\textwidth}|p{0.17\textwidth}|p{0.22\textwidth}|p{0.17\textwidth}|}
\hline
Размерность системы &Компилятор Фортрана &Время счёта, с &Компилятор С(С++) &Время счёта, с\\\hline
1000&gfortran &3.78 &g++ &0.89\\\hhline{~----}
&ifort &3.9 &icpc &0.88\\\hhline{~----}
&pgfortran &1.44 &pgc++ &0.85\\\hline
2000 &gfortran &34.37 &g++ &10.10\\\hhline{~----}
&ifort &33.02 &icpc &10.11\\\hhline{~----}
&pgfortran &16.13 &pgc++ &9.95\\\hline
\end{tabular}
\end{center}
\end{table}
</latex>
Как видно из результатов, программы на СC++ работают значительно быстрее, что является следствием большого количества
циклов в алгоритме.
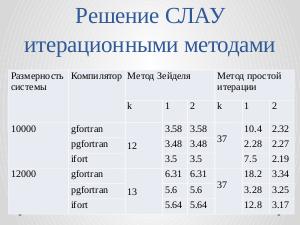
При написании последовательных приложений решения задач вычислительной математики использование конвейерных операций
позволяет значительно повысить быстродействие приложений. Авторами было проведено тестирование метода Зейделя и метода
простой итерации (см. табл.~3, в таблице <tt>k</tt> — "--- количество итераций, <tt>1</tt> — "--- программа с использованием циклов, <tt>2</tt> — "--- программа с
использованием конвейерных операций).
{| class="wikitable" style="font-size:85%; text-align:center;"
|+ '''Время счёта программ решения СЛАУ итерационными методами.'''
|-
! Размерность системы !! Компилятор !! colspan="3" | Метод Зейделя !! colspan="3" | Метод простой итерации
|-
! !! !! <tt>k</tt> !! 1 !! 2 !! <tt>k</tt> !! 1 !! 2
|-
| 10000 || gfortran || 12 || 3.58 || 3.58 || 37 || 10.4 || 2.32
|-
| || pgfortran || || 3.48 || 3.48 || || 2.28 || 2.27
|-
| || ifort || || 3.5 || 3.5 || || 7.5 || 2.19
|-
| 12000 || gfortran || 13 || 6.31 || 6.31 || 37 || 18.2 || 3.34
|-
| || pgfortran || || 5.6 || 5.6 || || 3.28 || 3.25
|-
| || ifort || || 5.64 || 5.64 || || 12.8 || 3.17
|}
<latex>
\begin{table}
\begin{center}
\tabcolsep=0.2em\scriptsize
\caption{\scriptsize Время счёта программ решения СЛАУ итерационными методами.}\label{aer-tbl02}
\begin{tabular}{|p{0.15\textwidth}|p{0.15\textwidth}|p{0.06\textwidth}|p{0.06\textwidth}|p{0.06\textwidth}|p{0.1\textwidth}|p{0.1\textwidth}|p{0.1\textwidth}|}
\hline
Размерность системы &Компилятор &\multicolumn{3}{c|}{Метод Зейделя} &\multicolumn{3}{c|}{Метод простой итерации}\\\hhline{~~------}
& &\multicolumn{1}{c|}{k} &\multicolumn{1}{c|}{1} &\multicolumn{1}{c|}{2} &\multicolumn{1}{c|}{k} &\multicolumn{1}{c|}{1} &\multicolumn{1}{c|}{2}\\\hline
10000 &gfortran &\multicolumn{1}{c|}{12} &3.58 &3.58 &\multicolumn{1}{c|}{37} &10.4 &2.32\\\hhline{~-~--~--}
&pgfortran & &3.48 &3.48 & &2.28 &2.27\\\hhline{~-~--~--}
&ifort & &3.5 &3.5 & &7.5 &2.19\\\hline
12000 &gfortran &\multicolumn{1}{c|}{13} &6.31 &6.31 &\multicolumn{1}{c|}{37} &18.2 &3.34\\\hhline{~-~--~--}
&pgfortran & &5.6 &5.6 & &3.28 &3.25\\\hhline{~-~--~--}
&ifort & &5.64 &5.64 & &12.8 &3.17\\\hline
\end{tabular}
\end{center}
\end{table}
</latex>
Значительное ускорение наблюдается, если удаётся написать код с использованием только матричных подпрограмм и операторов
(без циклов). При совместном использовании обычных циклов и матричных операции ускорение работы программы оказывается
незначительным.
Коммерческий проприетарный компилятор pgfortran генерирует быстродействующее параллельное приложение при написании
программы без использования современных матричных операторов и подпрограмм.
Если внимательно проанализировать результаты, представленные в табл.~3предыдущей таблице, можно заметить, что, не смотря на то, что метод
Зейделя требует значительно меньшее количество итераций, время счёта в методе простой итерации значительно меньше, чем
в методе Зейделя. Это связано с тем, что в методе Зейделя невозможно избавиться от последовательных циклов и перейти
полностью к матричным (конвейерным) операциям и подпрограммам. Алгоритм сложения является рекуррентным, что не
позволяет избавиться от последовательных циклов.
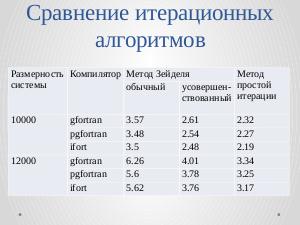
Однако можно ускорить алгоритм Зейделя при написании кода на Фортране, используя операцию матричного умножения <tt>matmul</tt>.
На каждой итерации можно предварительно умножать фрагмент матрицы на вектор $x$''x''. Это позволит сократить время счёта.
Платой за это будет память для хранения второй матрицы размерности $n\times n$''n × n''. Ниже приведены результаты сравнения
быстродействия обычного и усовершенствованного метода Зейделя и метода простой итерации.
{| class="wikitable" style="font-size:85%; text-align:center;"
|+ '''Быстродействие метода Зейделя, усовершенствованного метода Зейделя и метода простой итерации.'''
|-
! Размерность системы !! Компилятор !! colspan="2" | Метод Зейделя !! Метод простой итерации
|-
! !! !! обычный !! усовершенствованный !!
|-
| 10000 || gfortran || 3.57 || 2.61 || 2.32
|-
| || pgfortran || 3.48 || 2.54 || 2.27
|-
| || ifort || 3.5 || 2.48 || 2.19
|-
| 12000 || gfortran || 6.26 || 4.01 || 3.34
|-
| || pgfortran || 5.6 || 3.78 || 3.25
|-
| || ifort || 5.62 || 3.76 || 3.17
|}
<latex>
\begin{table}
\begin{center}
\tabcolsep=0.2em\scriptsize
\caption{\scriptsize Быстродействие метода Зейделя, усовершенствованного метода Зейделя и метода простой итерации.}\label{aer-tbl03}
\begin{tabular}{|p{0.17\textwidth}|p{0.2\textwidth}|p{0.17\textwidth}|p{0.17\textwidth}|p{0.17\textwidth}|}\hline
Размерность системы &Компилятор &\multicolumn{2}{c|}{Метод Зейделя} &Метод простой итерации\\\hhline{~~--~}
& &обычный &\multicolumn{1}{p{0.2\textwidth}|}{усовершенство\-ванный} &\\\hline
10000 &gfortran &3.57 &2.61 &2.32\\\hhline{~----}
&pgfortran &3.48 &2.54 &2.27\\\hhline{~----}
&ifort &3.5 &2.48 &2.19\\\hline
12000 &gfortran &6.26 &4.01 &3.34\\\hhline{~----}
&pgfortran &5.6 &3.78 &3.25\\\hhline{~----}
&ifort &5.62 &3.76 &3.17\\\hline
\end{tabular}
\end{center}
\end{table}
</latex>
Аналогичным образом можно ускорять и другие алгоритмы вычислительной математики, в которых используются матричные
операции.
Одним из новейших методов построения параллельных программ является технология автораспараллеливания,
полноценная поддержка которой реализована в только проприетарных компиляторах Intel посредством опций командной строки
<tt>-parallel</tt>.
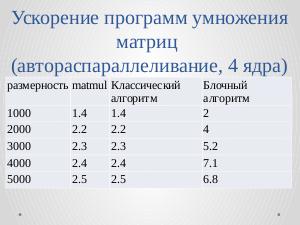
В таблице 5Ниже приведены результаты применения опции
автораспараллеливания к последовательным программам умножения матриц (matmul, классический и блочный
алгоритмы).
{| class="wikitable" style="font-size:85%; text-align:center;"
|+ '''Ускорение в программах умножения матриц с опцией автораспараллеливания (4 ядра).'''
|-
! Размерность !! matmul !! Классический алгоритм !! Блочный алгоритм
|-
| 1000 || 1.4 || 1.4 || 2
|-
| 2000 || 2.2 || 2.2 || 4
|-
| 3000 || 2.3 || 2.3 || 5.2
|-
| 4000 || 2.4 || 2.4 || 7.1
|-
| 5000 || 2.5 || 2.5 || 6.8
|}
<latex>
\begin{table}
\begin{center}
\tabcolsep=0.2em\scriptsize
\caption{\scriptsize Ускорение в программах умножения матриц с опцией автораспараллеливания (4 ядра).}\label{aer-tbl04}
\begin{tabular}{|p{0.2\textwidth}|p{0.2\textwidth}|p{0.2\textwidth}|p{0.2\textwidth}|}\hline
размерность &matmul &Классический алгоритм &Блочный алгоритм\\\hline
1000 &1.4 &1.4 &2\\\hline
2000 &2.2 &2.2 &4\\\hline
3000 &2.3 &2.3 &5.2\\\hline
4000 &2.4 &2.4 &7.1\\\hline
5000 &2.5 &2.5 &6.8\\\hline
\end{tabular}
\end{center}
\end{table}
</latex>
Кроме поддерживаемых в других языках программирования технологий параллельного программирования OpenMP
и MPI, в новый стандарт языка Fortran-2008 включены встроенные средства распараллеливания Co-Arrays (комассивы),
которые могут быть реализованы в системах как с распределенной, так и с общей памятью.
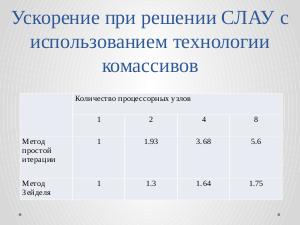
С помощью комассивов были разработаны параллельные реализации методов Зейделя и простой итерации. Оценка времени работы
программ приведена в таблице~
{| class="wikitable" style="font-size:85%; text-align:center;"
|+ '''Ускорение при решении СЛАУ размерности 7000 с использованием технологии комассивов на компьютерном кластере ВятГУ.'''
|-
! !! colspan="4" | Количество процессорных узлов
|-
! !! 1 !! 2 !! 4 !! 8
|-
| Метод простой итерации || 1 || 1.93 || 3.68 || 5.6.
|-
| Метод Зейделя || 1 || 1.3 || 1.64 || 1.75
|}
<latex>
\begin{table}
\begin{center}
\tabcolsep=0.2em\scriptsize
\caption{\scriptsize Ускорение при решения СЛАУ размерности 7000 и с использованием технологии комассивов на компьютерном кластере ВятГУ.}\label{aer-tbl05}
\begin{tabular}{|p{0.3\textwidth}|p{0.1\textwidth}|p{0.1\textwidth}|p{0.1\textwidth}|p{0.1\textwidth}|}\hline
&\multicolumn{4}{p{0.4\textwidth}|}{Количество процессорных узлов}\\\hhline{~----}
&1 &2 &4 &8\\\hline
Метод простой итерации & 1 & 1.93 & 3.68 & 5.6\\\hline
Метод Зейделя & 1 & 1.3 & 1.64 & 1.75\\\hline
\end{tabular}
\end{center}
\end{table}
</latex>
Современные компиляторы Фортрана позволяют разрабатывать высокоэффективный код
решения вычислительных задач с использованием современных технологий. Самые новые технологии параллельного
программирования полноценно поддерживаются на сегодняшний день только проприетарными компиляторами. При разработке
последовательных и параллельных приложений имеет смысл использовать последние версии свободного компилятора gfortran,
который генерирует самый быстрый код при работе с матрицами.
</latex>
{{LinksSection}}
<!-- <blockquote>[©]</blockquote> -->
<references/>
{{stats|disqus_comments=0|refresh_time=2020-01-22T20:56:29.3532502021-08-31T17:08:23.735260|vimeo_plays=247|youtube_comments=1|youtube_plays=3151055}}
[[Категория:OSEDUCONF-2018]]
[[Категория:Fortran]]
[[Категория:СПО в науке]]
[[Категория:High Performace Computing]] | |||
Текущая версия на 06:52, 20 октября 2025
- Докладчик
- Вячеслав Стародумов
Представлен обзор основных возможностей современных компиляторов (gfortran, ifort) языка Фортрана при решении вычислительных задач.
Содержание
Видео[править вики-текст]
Презентация[править вики-текст]
Thesis[править | править вики-текст]
Фортран — первый язык программирования высокого уровня, ориентированный на решение вычислительных задач. Современный Фортран в первую очередь ориентирован на высокоэффективные вычисления.
Среди основных нововведений Фортрана можно выделить:
- поддержка длинных чисел (шестнадцатибайтные целые и вещественные тридцатидвухбайтные комплексные числа);
- динамические массивы переменной длины;
- все основные операции, процедуры и функции языка выполняются не только над скалярными величинами, но и над массивами, матрицами, а также их фрагментами — секциями[1];
- в современных компиляторах реализована конвейерная обработка операций и функций над массивами и секциями, благодаря чему исполняемый код программ обработки массивов и матриц, генерируемый компиляторами Фортрана, является самым быстрым;
- поддержка параллельных вычислений на уровне стандарта языка: параллельные циклы, комассивы;
- поддержка технологий параллельного программирования MPI, OpenMP;
- внедрение технологии автораспараллеливания в компиляторе ifort.
Многие экономические, инженерные и вычислительные задачи сводятся к задачам умножения матриц и решению систем линейных алгебраических уравнений большой размерности. Рассмотрим, какие возможности предоставляют современные компиляторы для решения этих задач.
При анализе быстродействия авторами использовались следующие компиляторы языка Фортран:
- свободный компилятор gfortran (ver 7.2), поддерживающий большинство возможностей современных стандартов языка; компилятор gfortran портирован в Windows;
- проприетарный компилятор компании Intel — ifort, входящий в состав комплекса проприетарных программ Intel Parallel Studio; компилятор доступен для бесплатного использования в некоммерческих целях преподавателями, студентами и научными работниками;
- компилятор pgfortran, входящий в состав PGI Edition, который поддерживает технологию CUDA; существует версия компиляторов семейства PGI — PGI Community Edition.
В очень многих вычислительных задачах необходимо выполнять матричные операции. Самой затратной матричной операцией является операция умножение матриц[2]. Авторами была проанализирована эффективность умножения матриц на современном Фортране. В Фортране присутствует встроенная подпрограмма умножения матриц matmul, в последней версии gfortran (gfortran-7) функция значительно оптимизирована. Ниже приведены результаты времени выполнения программ, реализующих классический и блочный алгоритмы умножения матриц и подпрограммы matmul.
| Компилятор | Классический алгоритм, порядок выполнения циклов | Блочный алгоритм (размер блока 16) |
matmul | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ijk | jik | kij | ikj | jki | kji | ||||
| 1536 | gfortran | 20.5 | 23.65 | 52.9 | 49.9 | 2.22 | 3.77 | 2 | 0.5 |
| ifort | 0.67 | 0.7 | 0.7 | 0.67 | 1.99 | 0.7 | 2.68 | 0.69 | |
| pgfortran | 1.86 | 2.05 | 2.05 | 1.9 | 1.9 | 2.08 | 5.64 | 0.91 | |
| 2048 | gfortran | 91.12 | 89.84 | 219.5 | 222.48 | 5.26 | 8.84 | 4.75 | 1.16 |
| ifort | 1.52 | 1.66 | 1.65 | 1.6 | 4.68 | 1.64 | 6.98 | 1.63 | |
| pgfortran | 4.46 | 4.86 | 4.91 | 4.54 | 4.54 | 4.51 | 61.78 | 2.19 | |
При использовании проприетарных компиляторов, не важно в каком порядке записывать циклы в коде программ умножения матриц. Компиляторы ifort, pgfortran, достаточно хорошо оптимизируют исходный код. При использовании gfortran программист должен аккуратно писать код, записывая циклы в оптимальном для данного языка порядке. Подпрограмма умножения матриц, сформированная с помощью процедуры matmul и скомпилированная с помощью gfortran оказалась быстрее любого другого кода (даже быстрее блочного алгоритма и алгоритма Штрассена). Авторы сравнивали быстродействие программ умножения, написанных с использованием классических циклов на С и Фортране. Программы на Фортране работают на 10–12% быстрее. Использование matmul и свободного компилятора позволяет ускорить работу программы ещё в несколько раз. Поэтому именно matmul и новый компилятор gfortran-7 следует использовать для решения задач, сводящихся к умножению матриц.
Одной из тестовых задач анализа быстродействия является метод Гаусса решения СЛАУ. Было проведено сравнение быстродействие программ на С и Фортране.
| Размерность системы | Компилятор Фортрана | Время счёта, с | Компилятор С(С++) | Время счёта, с |
|---|---|---|---|---|
| 1000 | gfortran | 3.78 | g++ | 0.89 |
| ifort | 3.9 | icpc | 0.88 | |
| pgfortran | 1.44 | pgc++ | 0.85 | |
| 2000 | gfortran | 34.37 | g++ | 10.10 |
| ifort | 33.02 | icpc | 10.11 | |
| pgfortran | 16.13 | pgc++ | 9.95 |
Как видно из результатов, программы на C++ работают значительно быстрее, что является следствием большого количества циклов в алгоритме.
При написании последовательных приложений решения задач вычислительной математики использование конвейерных операций позволяет значительно повысить быстродействие приложений. Авторами было проведено тестирование метода Зейделя и метода простой итерации (в таблице k — количество итераций, 1 — программа с использованием циклов, 2 — программа с использованием конвейерных операций).
| Размерность системы | Компилятор | Метод Зейделя | Метод простой итерации | ||||
|---|---|---|---|---|---|---|---|
| k | 1 | 2 | k | 1 | 2 | ||
| 10000 | gfortran | 12 | 3.58 | 3.58 | 37 | 10.4 | 2.32 |
| pgfortran | 3.48 | 3.48 | 2.28 | 2.27 | |||
| ifort | 3.5 | 3.5 | 7.5 | 2.19 | |||
| 12000 | gfortran | 13 | 6.31 | 6.31 | 37 | 18.2 | 3.34 |
| pgfortran | 5.6 | 5.6 | 3.28 | 3.25 | |||
| ifort | 5.64 | 5.64 | 12.8 | 3.17 | |||
Значительное ускорение наблюдается, если удаётся написать код с использованием только матричных подпрограмм и операторов (без циклов). При совместном использовании обычных циклов и матричных операции ускорение работы программы оказывается незначительным.
Коммерческий проприетарный компилятор pgfortran генерирует быстродействующее параллельное приложение при написании программы без использования современных матричных операторов и подпрограмм.
Если внимательно проанализировать результаты, представленные в предыдущей таблице, можно заметить, что, не смотря на то, что метод Зейделя требует значительно меньшее количество итераций, время счёта в методе простой итерации значительно меньше, чем в методе Зейделя. Это связано с тем, что в методе Зейделя невозможно избавиться от последовательных циклов и перейти полностью к матричным (конвейерным) операциям и подпрограммам. Алгоритм сложения является рекуррентным, что не позволяет избавиться от последовательных циклов.
Однако можно ускорить алгоритм Зейделя при написании кода на Фортране, используя операцию матричного умножения matmul. На каждой итерации можно предварительно умножать фрагмент матрицы на вектор x. Это позволит сократить время счёта. Платой за это будет память для хранения второй матрицы размерности n × n. Ниже приведены результаты сравнения быстродействия обычного и усовершенствованного метода Зейделя и метода простой итерации.
| Размерность системы | Компилятор | Метод Зейделя | Метод простой итерации | |
|---|---|---|---|---|
| обычный | усовершенствованный | |||
| 10000 | gfortran | 3.57 | 2.61 | 2.32 |
| pgfortran | 3.48 | 2.54 | 2.27 | |
| ifort | 3.5 | 2.48 | 2.19 | |
| 12000 | gfortran | 6.26 | 4.01 | 3.34 |
| pgfortran | 5.6 | 3.78 | 3.25 | |
| ifort | 5.62 | 3.76 | 3.17 | |
Аналогичным образом можно ускорять и другие алгоритмы вычислительной математики, в которых используются матричные операции.
Одним из новейших методов построения параллельных программ является технология автораспараллеливания, полноценная поддержка которой реализована в только проприетарных компиляторах Intel посредством опций командной строки -parallel.
Ниже приведены результаты применения опции автораспараллеливания к последовательным программам умножения матриц (matmul, классический и блочный алгоритмы).
| Размерность | matmul | Классический алгоритм | Блочный алгоритм |
|---|---|---|---|
| 1000 | 1.4 | 1.4 | 2 |
| 2000 | 2.2 | 2.2 | 4 |
| 3000 | 2.3 | 2.3 | 5.2 |
| 4000 | 2.4 | 2.4 | 7.1 |
| 5000 | 2.5 | 2.5 | 6.8 |
Кроме поддерживаемых в других языках программирования технологий параллельного программирования OpenMP и MPI, в новый стандарт языка Fortran-2008 включены встроенные средства распараллеливания Co-Arrays (комассивы), которые могут быть реализованы в системах как с распределенной, так и с общей памятью.
С помощью комассивов были разработаны параллельные реализации методов Зейделя и простой итерации.
| Количество процессорных узлов | ||||
|---|---|---|---|---|
| 1 | 2 | 4 | 8 | |
| Метод простой итерации | 1 | 1.93 | 3.68 | 5.6 |
| Метод Зейделя | 1 | 1.3 | 1.64 | 1.75 |
Современные компиляторы Фортрана позволяют разрабатывать высокоэффективный код решения вычислительных задач с использованием современных технологий. Самые новые технологии параллельного программирования полноценно поддерживаются на сегодняшний день только проприетарными компиляторами. При разработке последовательных и параллельных приложений имеет смысл использовать последние версии свободного компилятора gfortran, который генерирует самый быстрый код при работе с матрицами.
Примечания и ссылки[править вики-текст]
- ↑ Секция массива — часть массива, которая определяется именем массива и границами изменения индексов (например,
x(:,4),y(1:15:3)). - ↑ Частным случаем матричного умножения являются — умножение матрицы на вектор и скалярное произведение векторов.
Plays:1102 Comments:1