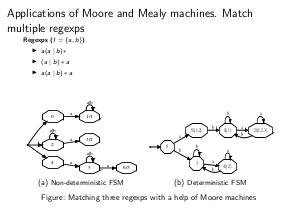
Applications of Finite State Machines (Алексей Чеусов, LVEE-2019) — различия между версиями

== Thesis ==
<latex>
Начать следует с определений и теорем, хорошо знакомых любому
выпускнику ВУЗ-а по технической специальности.

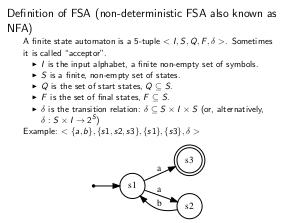
\textbf{Определение:} Недетерминированным конечным автоматом \linebreak (НКА) называется пятерка
\mbox{$<I,S,Q,F,\delta>$}, где
\begin{itemize}
\item $I$ — -- конечное непустое множество символов (алфавит);
\item $S$ — -- конечное непустое множество состояний;
\item $Q$ — -- множество стартовых состояний, $Q \subseteq S$;
\item $F$ — -- множество конечных состояний, $F \subseteq S$;
\item $\delta$ — -- отношение переходов $\delta \subseteq S \times I \times S$
  (или, иначе, $\delta: S \times I \rightarrow 2^S$).
\end{itemize}
</latex>
<latex>
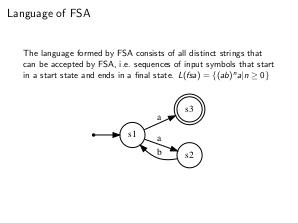
Языком КА является множество различных последовательностей символов алфавита, допускаемых
конечным автоматом, т.е.то есть, цепочек символов вдоль пути от стартового до конечного состояния КА.

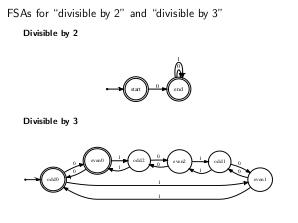
\textbf{Определение:} Регулярный язык над алфавитом $\Sigma$ определяется следующим образом:
\begin{itemize}
\item Пустой язык $\emptyset$ и язык $\{\epsilon\}$, состоящий из пустой строки, является регулярным языком;
\item $\{a\}$, где $a \in \Sigma$, является регулярным языком;
\item Если $A$ и $B$ регулярные языки, то $A \cup B$ (объединение), $A \bullet B$ (конкатенация),
  и $A\ast$ (звезда Клини) являются регулярными языками;
\item Никакие другие языки над $\Sigma$ не являются регулярными.
\end{itemize}
Этот формализм дает нам так называемые <<«регулярные выражения>>».

\textbf{Определение:} Детерминированным конечным автоматом \linebreak (ДКА) является пятерка $<I,S,q,F,\delta>$, где
\begin{itemize}
\item $I$ — -- конечное непустое множество символов (алфавит);
\item $S$ — -- конечное непустое множество состояний;
\item $q$ — -- стартовое состояние, $q \in S$.
\item $F$ — -- множество конечных состояний, $F \subseteq S$.
\item $\delta$ — -- функция переходов: $\delta: S \times I \rightarrow S$
\end{itemize}

</latex>
<latex>
\textbf{Теоремы}:
\begin{itemize}
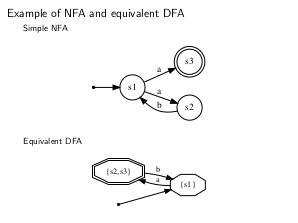
\item НКА и ДКА — -- эквивалентные формализмы, т.е.то есть, для каждого НКА
  существует эквивалентный ему ДКА, обратное верно по определению.
\item В общем случае ДКА может быть экспоненциально больше (по
  количеству состояний) по сравнению с эквивалентным ему НКА.
\item Для любого ДКА существует только один (с точностью до изоморфизма) минимальный ДКА,
  эквивалентный ему.
\item Регулярные языки и конечные автоматы — -- эквивалентные
  формализмы, то есть, для любого КА существует эквивалентный ему
  регулярный язык и наоборот.
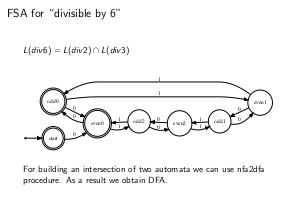
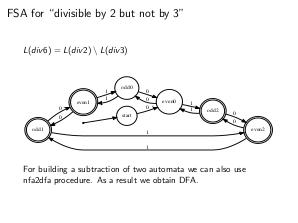
\item Конечные автоматы замкнуты относительно операций объединения, вычитания, пересечения, дополнения
  и звезды Клини.
\end{itemize}
</latex>

-----
<latex>
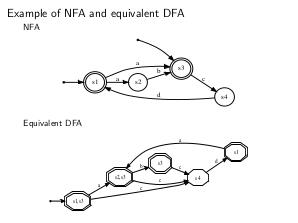
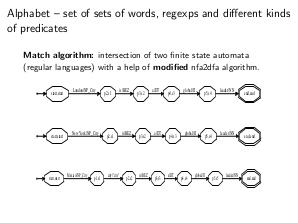
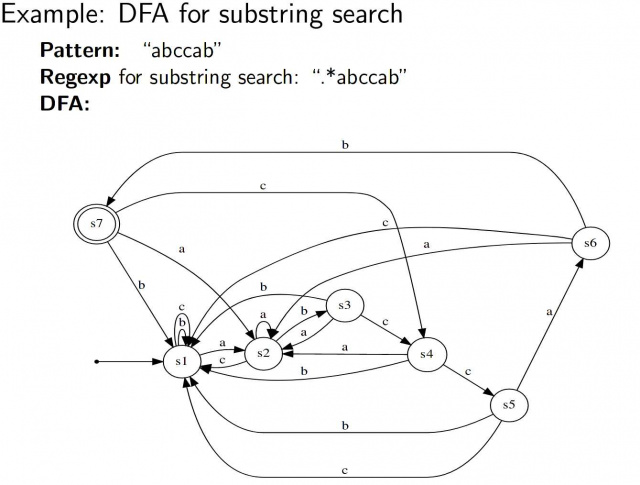
\textbf{Алгоритм} построения ДКА из НКА представлен ниже.
\begin{algorithm}[h!]
  \DontPrintSemicolon
  \SetKwInOut{Input}{input}
  \SetKwInOut{Output}{output}
  \Input{NFA = $<I,S,Q,F,\delta>$}
  \Output{DFA = $<I,S^{\prime},q^\prime,F^{\prime},\delta^{\prime}>$}
  \SetAlgoLined
%  \SetAlgoNoEnd
  $\delta^\prime := \emptyset, q^\prime := \{s | s \in Q\}, S^\prime := \{q^\prime\}$\;
  $seen := \{q^\prime\}, queue := [q^\prime]$\;
  \While{$queue \neq \emptyset$}{
    $src\_states \leftarrow queue$\;
    \For{$i \in I$}{
      $trg\_states := \{s^{trg} | (s^{src},i,s^{trg}) \in \delta, s^{src} \in src\_states\}$\;
      \If{$trg\_states \neq \emptyset$}{
        $\delta^\prime \leftarrow (src\_states, i, trg\_states)$\;
        $S^\prime \leftarrow trg\_states$\;
        \If{$trg\_states \notin seen$}{
          $queue \leftarrow trg\_states$\;
          $seen \leftarrow trg\_states$\;
        }
      }
    }
  }
  $F^\prime := \{state\_set \in S^\prime | \exists s \in state\_set, s \in F\}$
  \caption{nfa2dfa algorithm AKA <<Subset construction>>}
\end{algorithm}
</latex>
----
<latex>
Введем два дополнительных оператора:
\begin{itemize}
\item R — -- оператор инвертирования. $L(R(KA)) = \{inverse(w) | w \in L(KA)\}$
\item D — -- оператор построения ДКА по НКА.
\end{itemize}

\textbf{Алгоритм} Бжозовского построения минимального ДКА по \linebreak НКА:\\
$MinDFA = (D \circ R \circ D \circ R) KA$

\textbf{Замечание:} В отличие от большинства других алгоритмов построения минимального ДКА, алгоритм
Бжозовского строит минимальный ДКА по НКА!

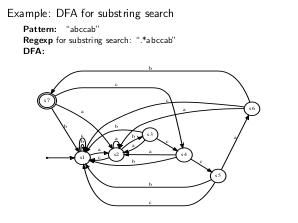
Алгоритм проверки, входит ли строка в язык ДКА.
</latex>

<latex>

\begin{algorithm}[h!]
  \DontPrintSemicolon
  \SetKwInOut{Input}{input}
  \SetKwInOut{Output}{output}
  \Input{DFA = $<I,S,q,F,\delta>, Text=[t_1, t_2 \dots t_n], t_i \in I$}
  \Output{$true$ \textbf{or} $false$}
  \SetAlgoLined
  %    \SetAlgoNoEnd
  $state := q$\;
  \For{$i$ from $1$ to $n$}{
    \uIf{$\delta$ is defined on $(state, t_i)$}{
      $state := \delta(state, t_i)$\;
    }\Else{
      \textbf{return} false\;
    }
  }
  \textbf{return} $(state \in F)$\;
  \caption{Сопоставление строки с ДКА. Сложность алгоритма: $O(n)$}
\end{algorithm}

Алгоритм проверки, входит ли строка в язык НКА.
\begin{algorithm}
  \DontPrintSemicolon
  \SetAlgoLined
  \SetKwInOut{Input}{input}
  \SetKwInOut{Output}{output}
  \Input{NFA = $<I,S,Q,F,\delta>, Text=[t_1, t_2 \dots t_n], t_i \in I$}
  \Output{$true$ \textbf{or} $false$}
  $states := Q$\;
  \For{$i$ from $1$ to $n$ \textbf{and} $states \neq \emptyset$}{
    $states := \{trg | (src, t_i, trg) \in \delta, src \in states\}$\;
  }
  \textbf{return} $(\exists s \in states, s \in F)$\;
  \caption{Сопоставление строки с НКА. Сложность алгоритма: $O(n * |S|)$}
\end{algorithm}

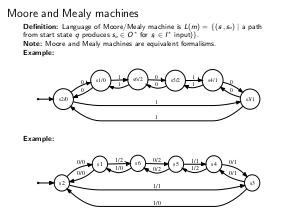
\textbf{Определение:}
Автомат Мура — -- это шестерка $<I,O,S,q,\delta, \lambda>$, где
\begin{itemize}
\item $I$ — -- входной алфавит, конечное непустое множество входных символов;
\item $O$ — -- выходной алфавит, конечное непустое множество выходных символов;
\item $S$ — -- конечное непустое множество состояний;
\item $q$ — -- стартовое состояние, $q \in S$;
\item $\delta$ — -- функция переходов $\delta: S \times I \rightarrow S$;
\item $\lambda$ — -- функция выходов $\lambda: S \rightarrow O$.
\end{itemize}

\textbf{Определение:}
Автомат Мили — -- это шестерка $<I,O,S,q,\delta, \lambda>$.
\begin{itemize}
\item $I$ — -- входной алфавит, конечное непустое множество входных символов;
\item $O$ — -- выходной алфавит, конечное непустое множество выходных символов;
\item $S$ — -- конечное непустое множество состояний;
\item $q$ — -- стартовое состояние, $q \in S$;
\item $\delta$ — -- функция переходов $\delta: S \times I \rightarrow S$
\item $\lambda$ — -- функция выходов $\lambda: S \times I \rightarrow O$
\end{itemize}
\textbf{Note:} На практике мы часто работаем с \textit{частично определенными} ДКА, НКА,
автоматами Мура и Мили, т.е.то есть, автоматами с частично определенной функцией переходов.

\textbf{Теорема:} Автоматы Мура и Мили — -- эквивалентные формализмы.

\textbf{Определение:} 
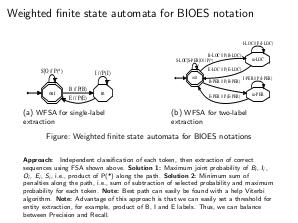
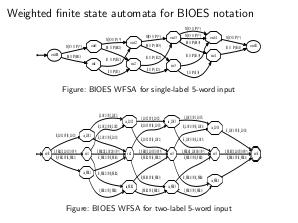
Взвешенный конечный автомат — -- это шестерка $<I,S,Q,F,\delta, \omega>$.
\begin{itemize}
\item $I$ — -- конечное непустое множество символов (алфавит);
\item $S$ — -- конечное непустое множество состояний;
\item $Q$ — -- множество стартовых состояний, $Q \subseteq S$;
\item $F$ — -- множество конечных состояний, $F \subseteq S$;
\item $\delta$ — -- отношение переходов $\delta \subseteq S \times I \times S$
\item $\omega: \delta \rightarrow \mathbb{R}$ — -- вес перехода.
\end{itemize}
$\omega$ может быть функцией расстояния, вероятностей, штрафов и  т. д., даже не обязательно $\mathbb{R}$.

\textbf{Определение:} Конечно-автоматный преобразователь — -- это шестерка
$<I,O,S,Q,F,\delta>$.
\begin{itemize}
\item $I$ — -- входной алфавит, конечное непустое множество входных символов;
\item $O$ — -- выходной алфавит, конечное непустое множество выходных символов;
\item $S$ — -- конечное непустое множество состояний;
\item $Q$ — -- множество стартовых состояний, $Q \subseteq S$;
\item $F$ — -- множество конечных состояний, $F \subseteq S$;
\item $\delta$ — -- отношение переходов $\delta \subseteq S \times (I \cup \{\epsilon\}) \times (O \cup \{\epsilon\})\times S$, где $\epsilon$ — -- это пустая строка.
\end{itemize}
\textbf{Замечание:} Взвешенный конечно-автоматный преобразователь \linebreak
определяется аналогично взвешенному конечному автомату.
</latex>
<latex>
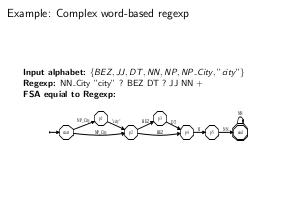
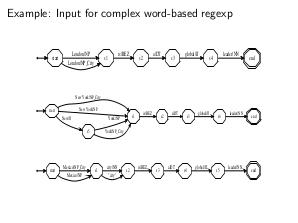
\textbf{Область применения взвешенных конечно-автоматных
  преобразователей:} распознавание речи, синтез речи, распознавание
символов, машинный перевод, различные задачи обработки естественного
языка, включая синтаксический анализ и моделирование языка,

</latex>
{{----}}
[[File:{{#setmainimage:Applications of Finite State Machines (Алексей Чеусов, LVEE-2019)!.jpg}}|center|640px]]
{{LinksSection}}
* Прежде всего хочется сказать, что данная статья является дополнением к презентации, доступной по ссылке ~
http://www.mova.org/~cheusov/pub/lvee/2019/fsa_presentation.pdf

* [ Talks page]
<!-- <blockquote>[©]</blockquote> -->
{{fblink|2427332600853080}}                                          
{{vklink|1456}}                                          
<references/>

{{stats|disqus_comments=1|refresh_time=2021-08-31T16:13:00.591899|vimeo_plays=11|youtube_comments=0|youtube_plays=61}}

[[Категория:LVEE-2019]]
[[Категория:Finite State Machines]]