Условные операторы — чуть теории для реализаторов (Николай Непейвода, OSSDEVCONF-2024)
Материал из 0x1.tv
- Докладчик
- Николай Непейвода
Нетривиальные сложности формализации условных операторов:
- с точки зрения теоретики — разных логик, разных моделей вычислений.
- и с точки зрения практиков.
Содержание
Видео[править вики-текст]
Презентация[править вики-текст]
Thesis[править | править вики-текст]
Напомним некоторые принципы понимания практиком теоретика[1].
- Если теоретик говорит, что это в принципе возможно, понимайте: это практически невозможно, нужно уточнить задачу.
- Если теоретик говорит, что это не имеет значения, понимайте: это имеет первостепенное значение для реализации.
- Если вы считаете, что теоретики занимаются сферическими конями в вакууме, говорить с ними бесполезно.
- Если вы осознали, что их мир другой, но имеет множество выходов на практику, надейтесь на успех.
В своей семье, где знают и теорию, и практику, мы порою называем теоретиков и практиков разными кастами. И у тех, и у других есть свой тайный язык, а общаться они могут лишь на общем, из-за этого понимают друг друга плохо.
Приведём два простейших примера перевода с теоретического на практический. Когда теоретик говорит, что операция коммутативна и ассоциативна (линейная логика Жирара[2]), то практик должен насторожиться и понять, что у него есть прекрасные возможности распараллеливания, организации распределённого поиска и оптимизации.
Ведь коммутативность и ассоциативность означает, что отдельные действия независимы, и их можно упорядочить или выполнять как угодно. Если же есть коммутативность без ассоциативности, то возникает неупорядоченное дерево, в котором можно так же распределить или оптимизировать движение, или же наоборот, быстро не задумываясь написать главный цикл или рекурсию, и заняться более интересными вещами.
Заметим, что всё время здесь появляется возможность распределённых вычислений, а свободные распределённые вычисления — это одно из направлений, где свободное программное обеспечение необходимо для слаженной работы волонтёров и решения трудных либо неразрешимых задач.
Здесь мы мельком коснулись ещё одного принципа работы с теоретиками.
Если теоретик говорит, что задача неразрешима или доказуемо трудна, то либо ограничьте аппетиты, выделив её часть, которая действительно нужна, либо поинтересуйтесь насчёт алгоритмов приближённого или вероятностного неточного решения.
В случае ограничения наилучшее разобраться с теоретиком, какие же подзадачи можно в принципе решить. Например, задача верификации программы доказуемо не проще, чем задача построения её с самого начала, что практически означает, что текст уже существующей программы будет чаще всего лишь мешать. Но задача верификации по типам данных или по областям изменения вполне решаемы и здесь текст программы помогает. Так что приходим к выводу Капитана Очевидность: проверить по настоящему можно лишь программу с открытым кодом, после чего ещё раз обращаемся к логикам и выясняем, что текста программы недостаточно в общем случае, нужно ещё иметь открытую спецификацию. И если это всё есть, практик может трудиться с большой надеждой на успех либо на обнаружение ловушек. Заметим, что в случае общей задачи верификации открытая спецификация помогает слабо (зато уж точно не мешает!), но зато она помогает аккуратно пересоздать подозрительную программу с самого начала.
А приближённый алгоритм часто прекрасно ложится на распределённые вычисления. Заметим только, что, если вы реализовали недетерминированность либо неточность псевдослучайным алгоритмом, то на самом деле это детерминированный алгоритм, и вы никакого выигрыша не получите.
Теперь рассмотрим один частный случай взаимодействия теории и практики: условные операторы.
Адекватный анализ условных вычислений требует обработки ошибок[3]. Поэтому логика здесь четырёхзначная. «T» и «F» нормальные значения, минимально требуемые для условных вычислений. «U» ошибка, которую можно попытаться обработать и продолжить вычисления, крах.
Традиционный условный оператор
if A then M else N fi
как показал Маккарти, является базисом алгоритмических вычислений над произвольными абстрактными типами данных. Рекурсивные схемы, состоящие из нескольких определений вида дают одно из самых удобных, мощных и абстрактных понятий вычислимости. Они создавались для случая последовательных вычислений, где единственный способ преодолеть ошибку — защититься от её появления соответствующим условием.
Дейкстра заметил, что, если задана спецификация программы, то более адекватен условный оператора вида (оригинальных обозначениях Дейкстра). выполняемый недетерминированно, поскольку в случае истинности нескольких условий нам безразлично, какую из возможностей выбрать. Но при реализации данный оператор обычно детерминируют, что дополнительно затрудняет верификацию, проверку и особенно модификацию программ: почему это стоит впереди ? Зато на распределённые вычисления дейкстровский оператор ложится прекрасно: задать волонтёрам свои и организовать «соревнование»: кто первым найдёт и вычислит удачный вариант?
Ещё одно очевидное и используемое, начиная с Фортрана, расширение условного оператора, когда управляющих значений не два , а несколько. Такие переключатели легко обобщаются до дейкстровских и поддаются соревновательным вычислениям.
Логика обычного оператора if также была описана Маккарти, и её называют логикой Лиспа. Она по умолчанию используется в большинстве реализаций логических связок. Поэтому потенциальная ошибка, а правильное выражение.
Группа Поттосина в ВЦ СО АН СССР заметила, что при параллельных вычислениях можно интерпретировать условный оператор по-другому. Вычисляем условие и обе альтернативы параллельно. Если условие никак не вычислится до конца либо даёт исправимую ошибку, но обе альтернативы дали один и тот же результат, то его и выдаём. С логической точки зрения это решение красивое и даёт логику Лукасевича, но практик здесь должен задуматься и скорее всего отвергнуть. Во-первых, это решение уменьшает шансы обойти ошибку, так как вычисляются все три части условного оператора. Во-вторых, оно плохо масштабируется на дейкстровский «if» и переключатели.
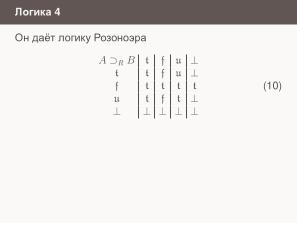
Если чисто логически попытаться развить новосибирскую идею, то приходим к максимальному «if». Если условие не вычисляется или даёт устранимую ошибку, и все альтернативы дают одно и то же значение либо устранимую ошибку, то принимаем выдаваемое значение. Этот вариант использован при управлении вычислениями по переполнениям, но он так же плохо обобщается на случаи дейкстровского оператора, переключателей и распределённых вычислений. Зато с логической точки зрения он даёт логику Розоноэра и функционально полон.
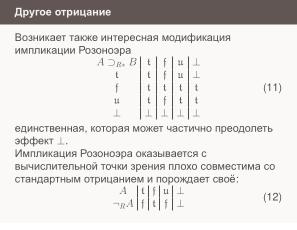
Ещё один вариант обработки ошибок — управление по неудачам, как в Прологе. Если условие дало ошибку, выбираем первую из альтернатив, давшую определённый результат. Этот вариант ориентирован на последовательное исполнение и также функционально полон с логической точки зрения. Он отлично обобщается на переключатели. Дейкстровский вариант такого оператора соответствует стандартной реализации case в языках, начиная с Лисп.
Таким образом, теоретический анализ в данном случае приводит к двум выводам. Во-первых, подтверждается целесообразность реализации стандартного либо прологовского варианта обработки условий. Во-вторых, в случае стандартного варианта традиционная реализация case является одной из подпорок, вставляемых для согласования с условностями реализации и затрудняющих анализ и модификацию программы.
Но саркастическая ошибка теоретического анализа состоит в том, что научной истины нет. Есть лишь условный вывод, базирующийся на массе допущений, многие из которых партнёры не высказывают вслух, причём умолчания разные, и поэтому они особенно коварны. В частности, если перейти к рекурсивным схемам, то здесь наиболее мощный результат, а также наибольшие возможности оптимизации, проверки и модификации даёт логически полный третий if. Прологовский формальную мощь даёт ту же, но возможности оптимизации и модификации хуже.
И, наконец, заметим, что непосредственно реализовать недетерминированность трудно, если вычисления не распределённые. Но практик может адекватно трактовать недетерминированность как разрешение детерминировать данное место любым способом, и использовать недетерминированный вариант как спецификацию либо даже разрешить его в языке с указанием, что транслятор имеет право детерминировать данный фрагмент любым способом, и оставить на усмотрение оптимизатора.
На самом деле в забытом ныне языке Алгол-68[4] было введено понятие совместного исполнения, когда операторы разделялись запятыми, что означало позволение транслятору вычислять их последовательно в любом порядке либо даже параллельно.
Примечания и ссылки[править вики-текст]
- ↑ Непейвода Н. Н. Математик и прикладник: о взаимо(не)понимании \\ Вестник Удмуртского университета, 2007, №1, стр. 251—268. \\EDN: [1]
- ↑ Emmanuel Beffara. Introduction to linear logic. Master. Italy. 2013. cel-01144229
- ↑ Непейвода Н. Н. Логики условных вычислений с ошибками. // Принята в журнал «Логические исследования» 2024.
- ↑ Пейган Ф. Дж. Практическое руководство по Алголу 68 = A Practical Guide to ALGOL 68 / пер. с англ. А. Ф. Рара, под ред. А. П. Ершова. — М.: Мир, 1979. — 240 с.