MROC3 — не магия, а справедливое слияние очередей (Елена Шамаева, OSEDUCONF-2021)
Материал из 0x1.tv
- Докладчик
- Елена Шамаева
Описывается применение в python алгоритма MROC3.
С его помощью для иерархии классов однозначным образом определяется очерёдность, в которой среди классов–предков происходит поиск поля. Такой упорядоченный линейный список классов–предков должен удовлетворять интуитивным ожиданиям программиста. В статье алгоритм сводится к справедливому слиянию очередей классов–предков, построенных для родительских классов. Разобраны принципы работы алгоритма, предложен новый метод визуализации объединения очередей.
Содержание
Видео
Презентация
Thesis
А люди всё роптали и роптали,
А люди справедливости хотят
В. С. Высоцкий
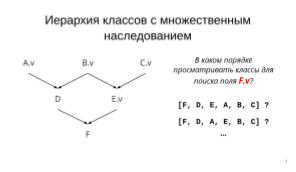
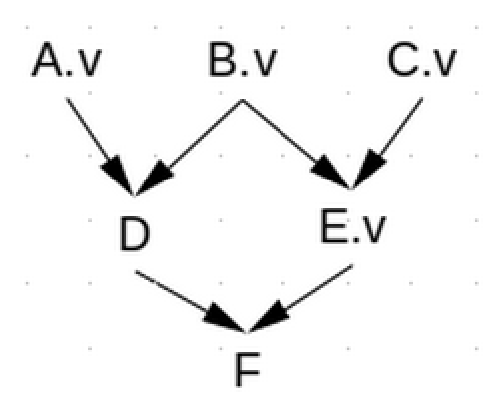
Появление в python множественного наследования усложнило алгоритм поиска поля, не определённого в классе–наследнике. Поскольку это поле могло быть определено в нескольких родительских классах (см. Рис. 1), появилась необходимость тем или иным способом определять очерёдность просмотра классов–предков.
Порядок просмотра классов удобно задавать с помощью линейного списка[1]: если удастся поместить в линейный список все классы из иерархии наследования, то при поиске поля достаточно будет последовательно просматривать эту очередь классов и выбирать первый попавшийся класс, содержащий данное поле. В python такой список формируется при создании класса и используется при обращении к любому из полей.
Начиная с версии 2.3, в python для решения этой проблемы используется алгоритм MROC3. Однако в статьях, описывающих этот алгоритм (например, и ) практически не объяснено, почему в результате данных действий с головами и хвостами различных списков получается искомый список классов, определяющий очерёдность их просмотра при поиске поля.
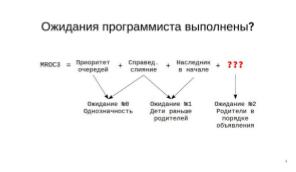
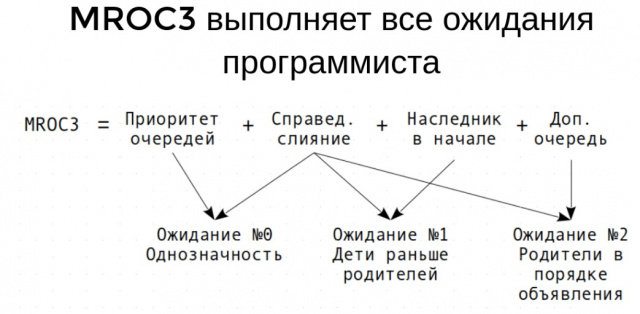
Список классов, построенный с помощью MROC3, удовлетворяет следующим интуитивным ожиданиям программиста:
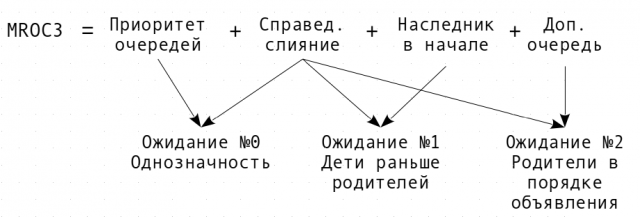
- Ожидание №0 — «однозначность»: порядок просмотра классов должен определяться однозначным образом, заданным иерархией классов;
- Ожидание №1 — «дети раньше родителей»: поиск поля сначала ведётся в дочерних классах, потом — в родительских;
- Ожидание №2 — «родители в порядке объявления при наследовании»: приоритетнее классы, стоящие левее при объявлении наследования.
Ожидание №1 задаёт на множестве классов частичный порядок: для двух классов, связанных отношением родители–дети, можно определить очерёдность просмотра при поиске поля. А Ожидание №0 устанавливает между классами отношение порядка, поскольку в однозначно построенном линейном списке для каждой пары классов можно установить очерёдность.
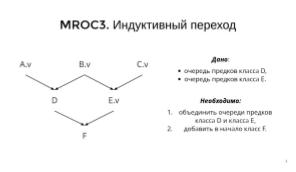
В алгоритме MROC3 линейный список классов строится индуктивно. Для класса, созданного без использования наследования, список состоит только из самого класса. При построении линейного списка для класса–наследника используются очереди, ранее построенные для его родительских классов. Сначала эти родительские очереди объединяются в одну, затем в начало объединённой очереди добавляется сам класс–наследник. При слиянии родительских очередей должен быть сохранён относительный порядок классов в каждой очереди, иначе для соответствующего родительского класса могут быть нарушены ожидания программиста.
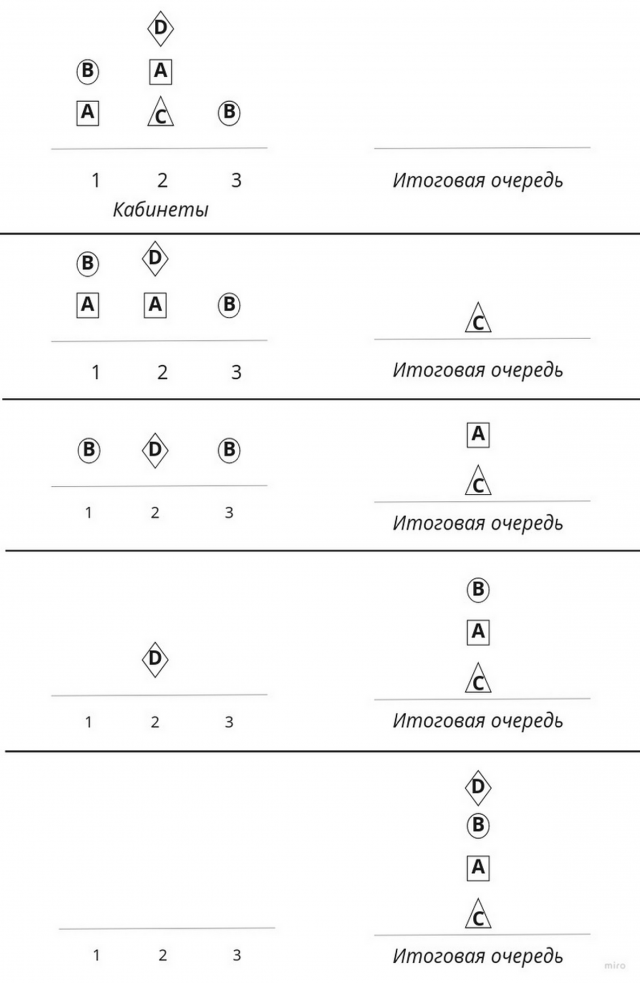
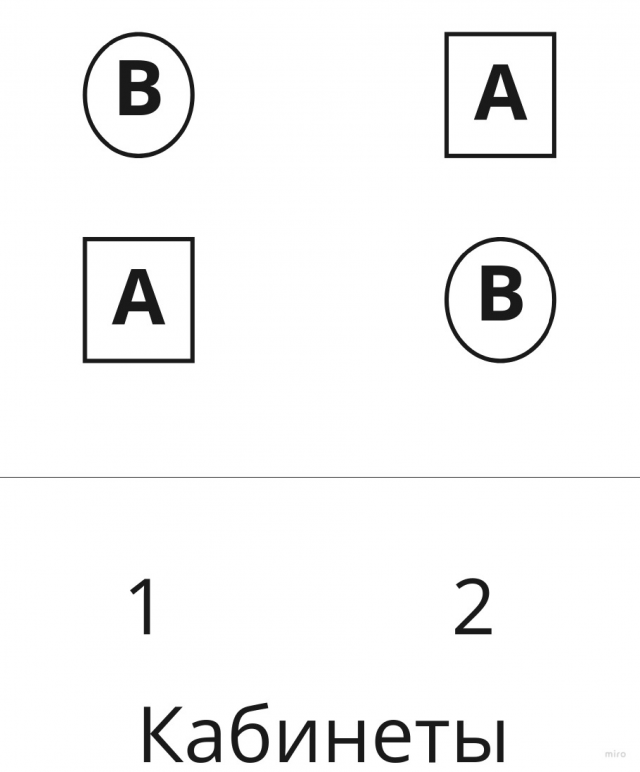
Слияние родительских очередей аналогично следующей ситуации. Допустим, в поликлинике необходимо объединить несколько очередей (причём каждый пациент ранее мог «занять место» сразу в нескольких очередях). Необходимо сделать так, чтобы никому не было обидно и никто не мог возмутиться: «Человек, ранее стоявший за мной, влез передо мной в итоговую очередь!» Пациент может быть перемещён в итоговую очередь только, если во всех очередях, в которых он стоит, перед ним нет других людей. Если несколько человек стоят первыми во всех своих очередях, приоритет — у людей из очереди в первый кабинет, потом — во второй кабинет и т.д. (см. Рис. 2). Такое справедливое слияние очередей сохраняет внутреннюю упорядоченность каждой очереди.
Если на каком–то этапе слияния люди блокируют друг друга (см. Рис. 3A), необходимо обратиться к заведующему поликлиникой[2].
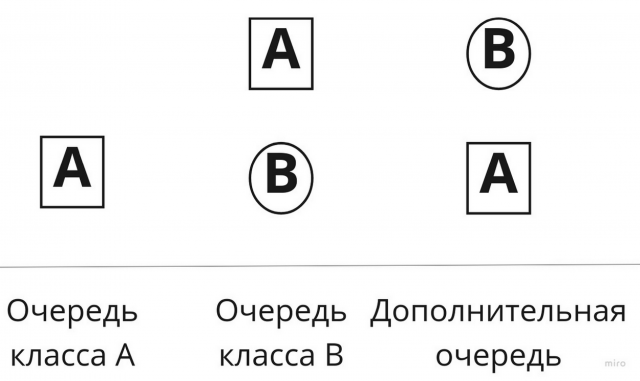
Для соблюдения Ожидания №2 создаётся дополнительная очередь из родительских классов в порядке их объявления при наследовании. За счёт справедливости слияния гарантируется соблюдение внутреннего порядка этой очереди (и, следовательно, порядка родительских классов при объявлении наследования)[3]. Эта дополнительная очередь также помогает обнаружить ситуацию, в которой Ожидания №1 и №2 противоречат друг другу. Например, для иерархии class A: class B(A): class C(A, B): (см. Рис. 3B).
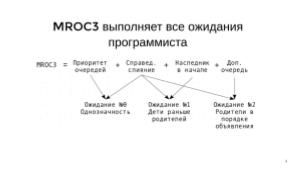
На схеме ниже (см. Рис. 4) показано, какие аспекты алгоритма MROC3 гарантируют соблюдение ожиданий программиста.
При визуализации на графе наследования очереди выглядят как разноцветные сосиски (начало очереди — снизу). Из этих «очередей–сосисок» классы постепенно перемещаются в итоговую очередь. При справедливом слиянии в неё могут быть перемещены только классы, стоящие в нижних концах всех своих очередей. Очередь считается «заблокированной», если её «нижний» класс содержится в середине другой очереди. На каждой итерации в итоговую очередь перемещается класс из первой по приоритету незаблокированной очереди.
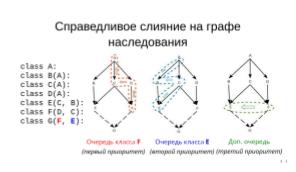
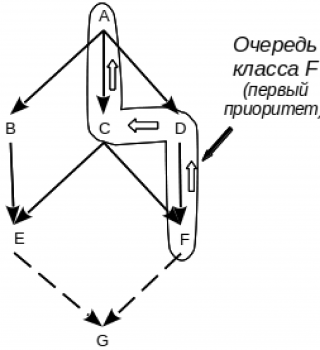
Например, при построении линейного списка для класса G из иерархии
class A: class B(A): class C(A): class D(A): class E(C, B): class F(D, C): class G(F, E):
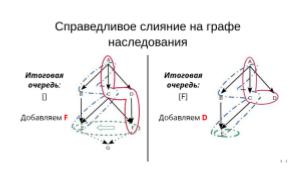
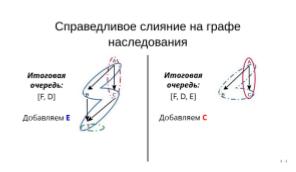
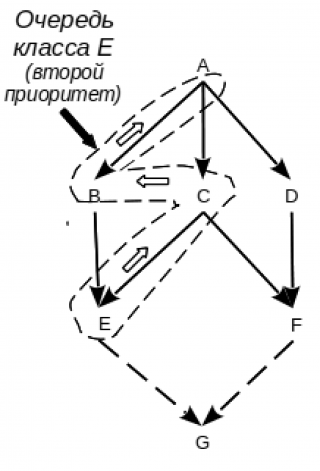
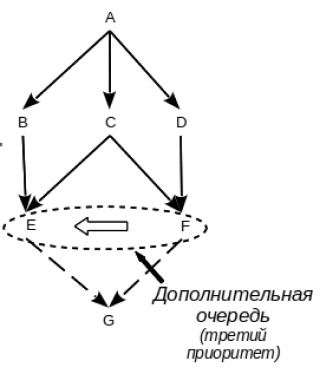
первый приоритет — у очереди класса F (см. Рис. 5A), второй — у очереди класса E (см. Рис. 5B)[4], третий — у дополнительной очереди родительских классов [F, E] (см. Рис. 5C). Родительскому классу F соответствует линейный список [F, D, C, A][5], родительскому классу E — [E, C, B, A].
В результате справедливого слияния будет построена очередь [G, F, D, E, C, B, A].
Алгоритм MROC3 строит линейный список классов, задающий порядок их просмотра для поиска поля из класса–наследника. Построение ведётся индуктивно, с помощью справедливого слияния очередей. Полученный список удовлетворяет интуитивным желаниям программиста. Для иллюстрации работы алгоритма была создана программная реализация .
- Probabilistic Inference II : https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-034-artificial-intelligence-fall-2010/lecture-videos/lecture-22-probabilistic-inference-ii/ (дата обращения: 04.06.2021) * Топологическая сортировка: https://habr.com/ru/post/100953/(дата обращения: 04.06.2021) Michele Simionato, The Python 2.3 Method Resolution Order, https://www.python.org/download/releases/2.3/mro/ type.__mro__: https://pythonz.net/references/named/type.__mro__/(дата обращения: 04.06.2021)
- Реализация MROC3: https://gist.github.com/Derinhelm/abd10f66ae505caded35861423959945 (дата обращения: 04.04.2021)
- ↑ Построение линейного списка вершин графа, удовлетворяющего некоторым условиям (линеаризация), — достаточно известная задача. Например, для Байесовских сетей, перед упрощением формул вероятности строится линейный список вершин графа событий. При топологической сортировке графа также необходимо задать линейный порядок на его вершинах.
- ↑ Для такой иерархии классов python генерирует TypeError
- ↑ В примере выше дополнительная очередь — это упорядоченная по приоритету кабинетов очередь из тех, кто стоял первый, когда врачи ушли (эти люди больше всех разозлились и будут пристальнее следить, чтобы лидер из низкоприоритетной очереди не встал раньше них).
- ↑ Приоритет очереди не связан с её местонахождением. При наследовании F стояло раньше E, то приоритет у очереди класса F выше.
- ↑ Строится слиянием очередей [D, A], [C, A], [D, C] и добавлением в начало класса F
Примечания и ссылки
Plays:0 Comments:0